Sección 2 Tipos de estudio y experimentos

Motivación

Pregunta de entrevista de Google (Chihara and Hesterberg 2018)
Imagina que eres consultor y te preguntan lo siguiente (ver siguiente figura):
Estoy haciendo una comparación de antes y después donde la hipótesis alternativa es pre.media.error > post.media.error. La distribución de ambas muestras es sesgada a la derecha. ¿Qué prueba me recomiendas para ésta situación?

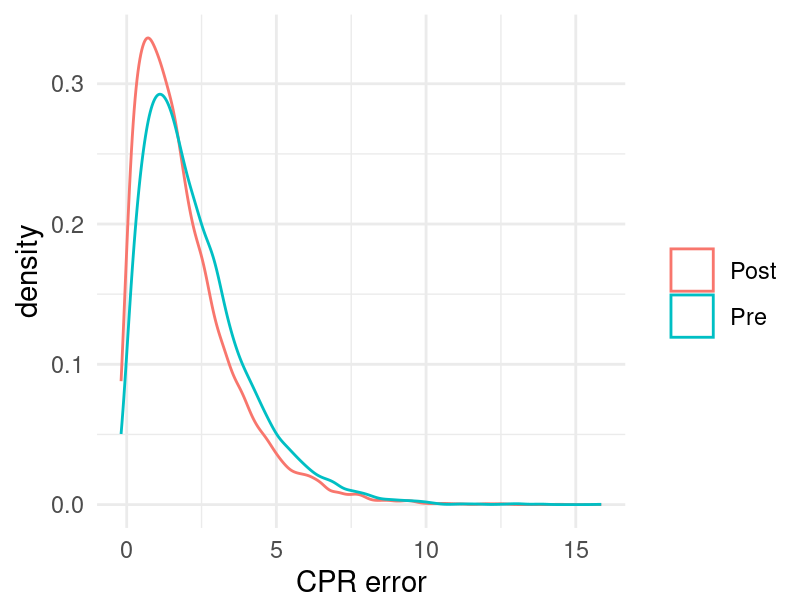
Figure 2.1: Error CPR, gráfica de densidad.

Far better an approximate answer to the right question, which is often vague, than an exact answer to the wrong question, which can always be made precise.

— John Tukey

La siguiente imagen Roger Peng representa una situación común a la que se enfrenta el analista de datos, y se desarrolló en el contexto de preguntas vagas. En el esquema hay tres caminos: uno es uno ideal que pocas veces sucede, otro produce respuestas poco útiles pero es fácil, y otro es tortuoso pero que caracteriza el mejor trabajo de análisis de datos:

Figure 2.2: Adaptado de R. Peng: Tukey, design thinking and better questions.

Ejemplos: Alguien nos pregunta cuáles son las tiendas que mas venden de una cadena. Podríamos consultar bases de datos, hacer extracciones, definir periodos, etc. y reportar el promedio de ventas en el último mes, esta respuesta probablemente es poco útil. Nos damos cuenta, por ejemplo, porque la peor tienda es una que abrió hace relativamente poco, y la mejor es una de las tiendas más grandes que está en una zona de tráfico de alto costo. Una pregunta más interesante es, ¿qué equipos de ventas tienen mejor desempeño? ¿Cuánto aporta tener una cafetería dentro de la tienda en términos de ventas?, etc.

Proceso Generador de Datos

Entre las preguntas que se debe hacer el analista de datos una fundamental es entender el proceso generador de datos, pues esto determinará que otras preguntas son relevantes, y que análisis son adecuados, tanto en términos prácticos como estadísticos.

• La inferencia estadística busca hacer afirmaciones, cuantificadas de manera probabilista, acerca de datos que no tenemos, usando regularidades y conocimiento de datos que sí tenemos disponibles y métodos cuantitativos.

• Para hacer afirmaciones inferenciales eficientes y bien calibradas (con garantías estadísticas de calibración) a preguntas donde queremos generalizar de muestra a población, se requiere conocer con precisión el proceso que genera los datos muestrales.

• Esto incluye saber con detalle cómo se seleccionaron los datos a partir de los que se quiere hacer inferencia.

En este caso, eficiente quiere decir que aprovechamos toda la información que está en los datos observados de manera que nuestros rangos de incertidumbre son lo más chico posibles (además de estar correctamente calibrados).

Por su parte, probabilísticamente bien calibrados se refiere a que, lo que decimos que puede ocurrir con 10% de probabilidad ocurre efectivamente 1 de cada 10 veces, si decimos 20% entonces ocurre 2 de 20, etc.

Veremos que para muestras dadas naturalmente, a veces es muy difiícil entender a fondo el proceso que generó la muestra y por tanto no tenemos las garantías de eficiencia y calibración.

Ejemplo: Prevalencia de anemia

Supongamos que nos interesa conocer el porcentaje de menores en edad escolar, (entre 6 y 15 años), con anemia en México. La fuente de datos disponible corresponde a registros del IMSS de hospitalizaciones de menores, ya sea por anemia o por otra causa (infecciones gastrointestinales, apendicitis, tratamiento de leucemia, …), se registró si el menor tenía anemia. En nuestra muestra el 47% de los niños tiene anemia.

head(paciente)
#> # A tibble: 6 × 4
#>    edad padecimiento         sexo   anemia
#>   <int> <chr>                <chr>   <int>
#> 1     8 picadura alacrán     mujer       0
#> 2    10 infección intestinal hombre      1
#> 3     7 mordedura de perro   hombre      1
#> 4     8 asma                 hombre      1
#> 5    13 infección intestinal mujer       0
#> 6     7 picadura alacrán     hombre      0

• ¿Qué nos dice esta cantidad acerca de la anemia en la población?
  
• ¿Podemos hacer inferencia estadística?
  
• ¿Cómo calculamos intervalos de confianza?

# Si calculo el error estándar de la p estimada como sigue, es correcto?
p <- mean(paciente$anemia)
sqrt(p * (1 - p) / 5000)
#> [1] 0.007060751

Muestreo aleatorio

En la situación ideal diseñaríamos una muestra aleatoria de menores de edad, por ejemplo, utilizando el registro en educación primaria de la SEP, y mediríamos la prevalencia de anemia en la muestra, usaríamos esta muestra para estimar la prevalencia en la población y tendríamos además las herramientas para medir la incertidumbre de nuestra estimación (reportar intervalos, o errores estándar).

El elemento clave, es la aleatorización en la selección de la muestra, la idea es distribuir los efecros desconcidos o no controlables que pueden introducir sesgos o variabilidad no conocida en los resultados.

Pero si no podemos hacer muestreo aleatorio?

En el caso de prevalencia de anemia, discutiendo con médicos e investigadores nos informan que la anemia se presenta en tasas más altas en niños más chicos.

paciente |> 
  count(edad) |> 
  mutate(prop = round(100 * n / sum(n)))
#> # A tibble: 10 × 3
#>     edad     n  prop
#>    <int> <int> <dbl>
#>  1     6  1001    20
#>  2     7   931    19
#>  3     8   980    20
#>  4     9   445     9
#>  5    10   484    10
#>  6    11   489    10
#>  7    12   246     5
#>  8    13   239     5
#>  9    14    90     2
#> 10    15    95     2

Y consultando con las proyecciones de población notamos que los niños chicos están sobrerepresentados en la muestra. Lo que nos hace considerar que debemos buscar una manera de ponderar nuestras observaciones para que reflejen a la población.

Más aún, investigamos que algunas enfermedades están asociadas a mayor prevalencia de anemia:

paciente |> 
  count(padecimiento) |> 
  arrange(-n)
#> # A tibble: 7 × 2
#>   padecimiento               n
#>   <chr>                  <int>
#> 1 infección respiratoria   745
#> 2 mordedura de perro       723
#> 3 úlcera                   723
#> 4 asma                     713
#> 5 apendcitis               704
#> 6 picadura alacrán         701
#> 7 infección intestinal     691

Utilizamos esta información para modelar y corregir nuestra estimación original. Por ejemplo con modelos de regresión. Sin embargo, debemos preguntarnos:

• ¿Hay más variables qué nos falta considerar?

Ejemplo: Policías y tráfico

Supongamos que nos preguntan en cuánto reduce un policía el tráfico en un crucero grande de la ciudad. La cultura popular ha establecido que los policías en cruceros hacen más tráfico porque no saben mover los semáforos.

Nosotros decidimos buscar unos datos para entender esto. Escogemos entonces un grupo de cruceros problemáticos, registramos el tráfico cuando visitamos, y si había un policía o no.

Después de este esfuerzo, obtenemos los siguientes datos:

#> # A tibble: 10 × 2
#> # Groups:   policia [2]
#>    policia tiempo_espera_min
#>      <int>             <dbl>
#>  1       0              2.27
#>  2       0              2.65
#>  3       0              3.4 
#>  4       0              0.39
#>  5       0              1.1 
#>  6       1             10.8 
#>  7       1              4.67
#>  8       1              7.77
#>  9       1              6.3 
#> 10       1              6.99

Lo que sabemos ahora es que la presencia de un policía es indicador de tráfico alto. El análisis prosiguiría calculando medias y medidas de error (escogimos una muestra aleatoria):

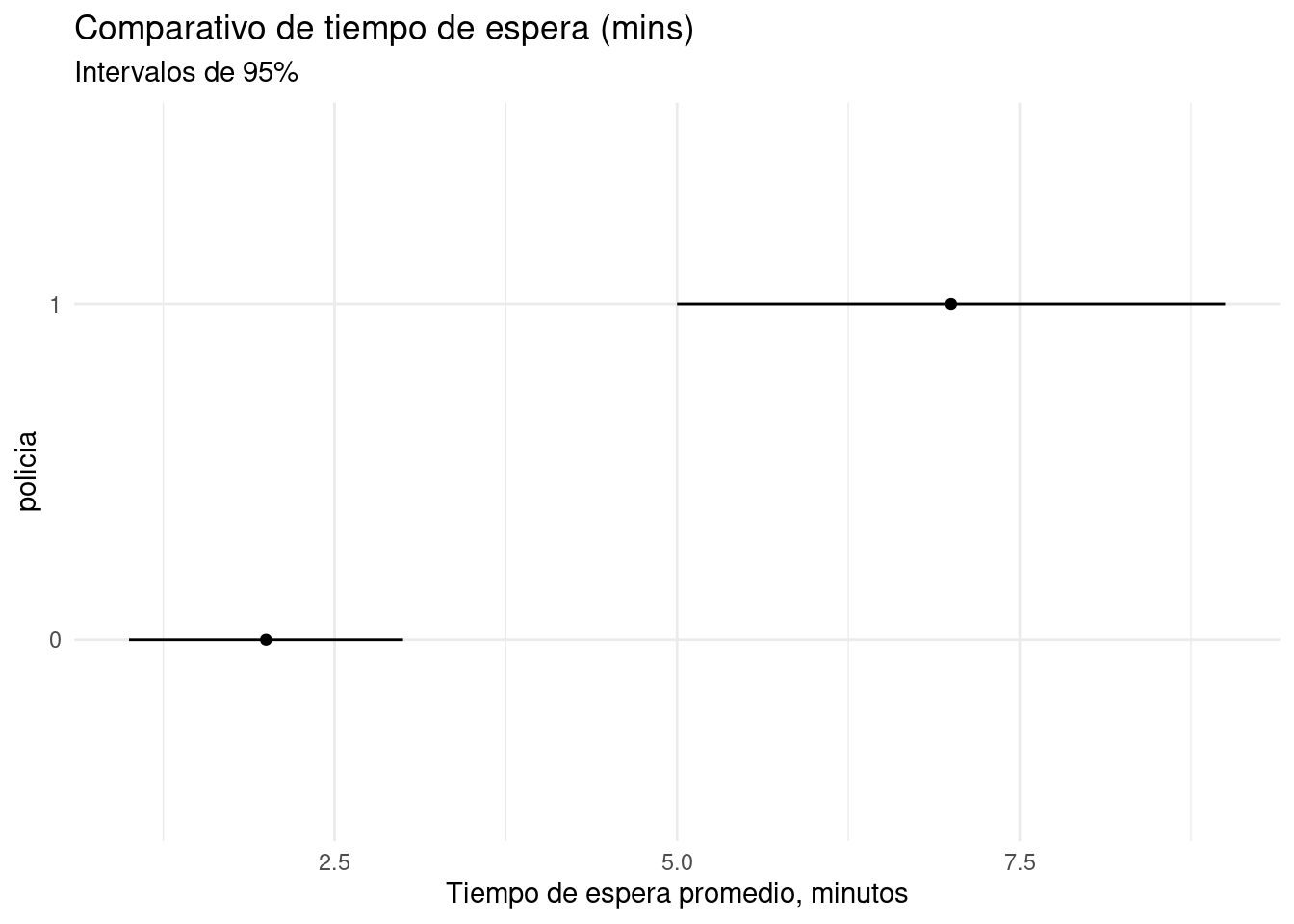
Si somos ingenuos, entonces podríamos concluir que los policías efectivamente empeoran la situación cuando manipulan los semáforos, y confirmaríamos la sabiduría popular.

Para juzgar este argumento desde el punto de vista causal, nos preguntamos primero:

• ¿Cuáles son los contrafactuales (los contrafactuales explican que pasaría si hubiéramos hecho otra cosa que la que efectivamente hicimos) de las observaciones?

Efectos causales y el esquema de resultados potenciales

Consideramos un tratamiento binario: Se manda policía o no se manda policía. Un resultado potencial es aquél que se observaría bajo un tratamiento particular. En cada semáforo, a una hora dada, hay dos resultados potenciales, uno por cada valor del tratamiento:

• \(y_1:\) tiempo de espera si se envía policía.

• \(y_0:\) tiempo de espera si no se envía policía.

Para cada semáforo, en el momento de registro, uno observa únicamente uno de los dos resultados potenciales. El resultado no observado se conoce como resultado contrafactual.

El estimador estándar

A la comparación anterior - la diferencia de medias de tratados y no tratados - le llamamos usualmente el estimador estándar del efecto causal. Muchas veces este es un estimador malo del efecto causal.

En nuestro ejemplo, para llegar a la conclusión errónea que confirma la sabiduría popular, hicimos un supuesto importante:

• En nuestra muestra, los casos con policía actúan como contrafactuales de los casos sin policía.
• Asi que asumimos que los casos con policía y sin policía son similares, excepto por la existencia o no de policía.

En nuestro ejemplo, quizá un analista más astuto nota que tienen categorías históricas de qué tan complicado es cada crucero. Junta a sus datos, y obtiene:

#> # A tibble: 10 × 3
#> # Groups:   policia [2]
#>    policia tiempo_espera_min categoria 
#>      <int>             <dbl> <fct>     
#>  1       0              2.27 Fluido    
#>  2       0              2.65 Fluido    
#>  3       0              3.4  Típico    
#>  4       0              0.39 Fluido    
#>  5       0              1.1  Fluido    
#>  6       1             10.8  Complicado
#>  7       1              4.67 Típico    
#>  8       1              7.77 Complicado
#>  9       1              6.3  Complicado
#> 10       1              6.99 Típico

El analista argumenta entonces que los policías se enviaron principalmente a cruceros que se consideran Complicados según datos históricos. Esto resta credibilidad a la comparación que hicimos inicialmente:

• La comparación del estimador estándar no es de peras con peras: estamos comparando qué efecto tienen los policías en cruceros difíciles, con cruceros no difíciles donde no hay policía.
• La razón de esto es que el proceso generador de los datos incluye el hecho de que no se envían policías a lugares donde no hay tráfico.
• ¿Cómo producir contrafactuales para hacer la comparación correcta?

Experimentos tradicionales

Idealmente, quisiéramos observar un mismo crucero en las dos condiciones: con y sin policías. Esto no es posible.

En un experimento “tradicional”, como nos lo explicaron en la escuela, nos aproximamos a esto preparando dos condiciones idénticas, y luego alteramos cada una de ellas con nuestra intervención. Si el experimento está bien hecho, esto nos da observaciones en pares, y cada quien tiene su contrafactual.

La idea del experimiento tradicional es controlar todos los factores que intervienen en los resultados, y sólo mover el tratamiento para producir los contrafactuales. Más en general, esta estrategia consiste en hacer bloques de condiciones, donde las condiciones son prácticamente idénticas dentro de cada bloque. Comparamos entonces unidades tratadas y no tratadas dentro de cada bloque.

Por ejemplo, si queremos saber si el tiempo de caída libre es diferente para un objeto más pesado que otro, prepararíamos dos pesos con el mismo tamaño pero de peso distinto. Soltaríamos los dos al mismo tiempo y compararíamos el tiempo de caída de cada uno.

En nuestro caso, como es usual en problemas de negocio o sociales, hacer esto es considerablemente más difícil. No podemos “preparar” cruceros con condiciones idénticas. Sin embargo, podríamos intentar \(bloquear\) los cruceros según información que tenemos acerca de ellos, para hacer más comparaciones de peras con peras.

Bloqueo

Podemos acercanos en lo posible a este ideal de experimentación usando información existente.

En lugar de hacer comparaciones directas entre unidades que recibieron el tratamiento y las que no (que pueden ser diferentes en otros aspectos, como vimos arriba), podemos refinar nuestras comparaciones bloquéandolas con variables conocidas.

En el ejemplo de los policías, podemos hacer lo siguiente: dentro de cada categoría de cruceros (fluido, típico o complicado), tomaremos una muestra de cruceros, algunos con policía y otros sin. Haremos comparaciones dentro de cada categoría.

Obtenemos una muestra con estas características (6 casos en cada categoría de crucero, 3 con policía y 3 sin policía):

categoria	policia	n
Fluido	0	3
Fluido	1	3
Típico	0	3
Típico	1	3
Complicado	0	3
Complicado	1	3

Y ahora hacemos comparaciones dentro de cada bloque creado por categoría:

#> # A tibble: 3 × 3
#> # Groups:   categoria [3]
#>   categoria  `policia =0` `policia =1`
#>   <fct>             <dbl>        <dbl>
#> 1 Fluido              2.1          0.8
#> 2 Típico              5.6          4.2
#> 3 Complicado         10.4          8.6

Y empezamos a ver otra imagen en estos datos: comparando tipos e cruceros similares, los que tienen policía tienen tiempos de espera ligeramente más cortos.

¿Hemos termniado? ¿Podemos concluir que el efecto de un policía es beneficiosos pero considerablemente chico? ¿Qué problemas puede haber con este análisis?

Variables desconocidas

El problema con el análisis anterior es que controlamos por una variable que conocemos, pero muchas otras variables pueden estar ligadas con el proceso de selección de cruceros para enviar policías.

• Por ejemplo, envían o policías a cruceros Típicos solo cuando reportan mucho tráfico.
• No envían a un polícia a un crucero Complicado si no presenta demasiado tráfico.
• Existen otras variables desconocidas que los tomadores de decisiones usan para enviar a los policías.

En este caso, por ejemplo, los expertos hipotéticos nos señalan que hay algunos cruceros que aunque problemáticos, a veces su tráfico se resuelve rápidamente, mientras que otros tienen tráfico más persistente, y prefieren enviar policías a los de tráfico persistente. La lista de cruceros persistentes están en una hoja de excel que se comparte de manera informal.

En resumen, no tenemos conocimiento detallado del proceso generador de datos en cuanto a cómo se asignan los policías a los cruceros.

Igual que en la sección anterior, podemos cortar esta complejidad usando aleatorización.

Nótese que los expertos no están haciendo nada malo: en su trabajo están haciendo el mejor uso de los recursos que tienen. El problema es que por esa misma razón no podemos saber el resultado de sus esfuerzos, y si hay maneras de optimizar la asignación que hacen actualmente.

Aleatorizando el tratamiento

Tomamos la decisión entonces de hacer un experimento que incluya aletorización.

En un dia particular, escogeremos algunos cruceros. Dicidimos usar solamente cruceros de la categoría Complicada y Típica, pues esos son los más interesantes para hacer intervenciones.

Usaremos un poco de código para entener el detalle: en estos datos, tenemos para cada caso los dos posibles resultados hipotéticos \(y_0\) y \(y_1\) (con policia y sin policia). En el experimento asignamos el tratamiento al azar:

muestra_exp <- trafico_tbl |> filter(categoria != "Fluido") |> 
  sample_n(200) |> 
  # asignar tratamiento al azar, esta es nuestra intervención:
  mutate(tratamiento_policia = rbernoulli(length(y_0), 0.5)) |>
  # observar resultado
  mutate(tiempo_espera_exp = ifelse(tratamiento_policia == 1, y_1, y_0))

Nótese la diferencia si tomamos la asignación natural del tratamiento (policía o no):

set.seed(134)
muestra_natural <- trafico_tbl |> filter(categoria != "Fluido") |>  
  sample_n(200) |> 
  # usamos el tratamiento que se asignó
  # policia indica si hubo o no policía en ese crucero
  # observar resultado
  mutate(tiempo_espera_obs = ifelse(policia == 1, y_1, y_0))

Resumimos nuestros resultados del experimento son:

#> # A tibble: 2 × 3
#> # Groups:   categoria [2]
#>   categoria  `policia=0` `policia=1`
#>   <fct>            <dbl>       <dbl>
#> 1 Típico            6.24        4.97
#> 2 Complicado       15.8         8.47

Sin embargo, la muestra natural da:

#> # A tibble: 2 × 3
#> # Groups:   categoria [2]
#>   categoria  `policia=0` `policia=1`
#>   <fct>            <dbl>       <dbl>
#> 1 Típico            5.49        4.35
#> 2 Complicado       10.8         8.93

¿Cuál de los dos análisis da la respuesta correcta a la pregunta: ayudan o no los policías a reducir el tráfico en los cruceros problemáticos? El experimento establece que un policía en promedio reduce a la mitad el tiempo de espera en un crucero complicado

Selección de unidades y tratamiento

Vimos dos tipos de inferencia que requieren distintos diseños de estudio: a poblaciones (ejemplo anemia) y causal (ejemplo policías). En el escenario ideal de cada uno de estos ejemplos requerimos un mecanismo de aleatorización, sin embargo, la aleatorización requerida en cada caso es distinta y distinguir esto es fundamental para entender las inferencias que podemos hacer en distintos escenarios.

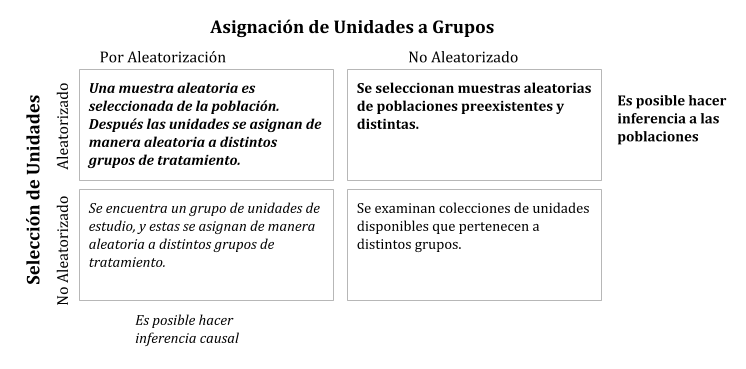
Inferencia estadística de acuerdo al tipo del diseño (Ramsey and Schafer (2012)).

• El cuadro arriba a la izquierda es donde el análisis es más simple y los resultados son más fáciles de interpretar. En este escenario don de la aleatorización es tanto en unidades como en grupos no hacen falta supuestos adicionales para tener las garantías de métodos de inferencia.

• Es posible hacer análisis fuera de este cuadro, pero el proceso es más complicado, requieren más supuestos, conocimiento del dominio y habilidades de análisis. En general resultan conclusiones menos sólidas. Muchas veces no nos queda otra más que trabajar fuera del cuadro ideal.

• El punto crucial para entender las medidas de incertidumbre estadística es visualizar de manera hipotética, replicaciones del estudio y las condiciones que llevaron a la selección de la muestra. Esto es, entender el proceso generador de datos e imaginar replicarlo.

Ubica los siguientes tipos de análisis:

• Pruebas clínicas para medicinas
• Analizar cómo afecta tener seguro médico a los ingresos, usando datos del ENIGH.
• Estimación de retorno sobre inversión en modelos de marketing mix.

Asignación natural del tratamiento

• Cuando consideramos un sistema donde se “asignan” tratamientos de manera natural, generalmente los tratamientos se asignan bajo un criterio de optimización o conveniencia (por ejemplo los policías a cruceros problemáticos).

• La cara buena de este hecho es que de alguna forma los resultados están intentando optimizarse, y la gente está haciendo su trabajo.

• La cara mala de este hecho es que no podemos evaluar de manera simple la efectividad de los tratamientos. Y esto hace difícil optimizar de forma cuantificable los procesos, o entender qué funciona y qué no.

Referencias

Chihara, Laura M., and Tim C. Hesterberg. 2018. Mathematical Statistics with Resampling and r. 2nd ed. Hoboken, NJ: John Wiley & Sons. https://sites.google.com/site/chiharahesterberg/home.

Ramsey, Fred, and Daniel Schafer. 2012. The Statistical Sleuth: A Course in Methods of Data Analysis. Cengage Learning.