8.6 Pruebas de hipótesis típicas

Antes de proseguir recordemos los conceptos de prueba de hipótesis:

1. Hipótesis nula (\(H_0\)): hipótesis que se desea contrastar, describe la conducta default del fenómeno de interés.

2. Hipótesis alternativa (\(H_1\)).

3. Estadística de prueba: es una estadística con base en la cuál tomamos la decisión de rechazar o no rechazar. Se calcula considerando la hipótesis nula como verdadera.

4. Valor-p: Nivel de significancia alcanzado, probabilidad de que la estadística de prueba sea al menos tan extrema como la observada con los datos si la hipótesis nula es verdadera.

Escenario	\(H_0\) verdadera	\(H_0\) Falsa
Rechazar \(H_0\)	Error Tipo 1 (\(\alpha\))	Decisión correcta
No rechazar \(H_0\)	Decisión correcta	Error tipo 2 (\(\beta\))

Ejemplo: estaturas

Usamos datos de estaturas, la hipótesis nula es que la media de las estaturas es la misma para hombres y mujeres. Hipótesis: \[H_0:\mu_m = \mu_h\] Estadistica de prueba es: \[Z=\frac{\bar{X_m}-\bar{X_h}}{\hat{\sigma}\sqrt{1/n_1+1/n_2}}\] la prueba se basa en una distribución \(t\) con \(n_1 + n_2 - 2\) grados de libertad.

heights_f <- singer_g$height[singer_g$gender == "F"]
heights_m <- singer_g$height[singer_g$gender == "M"]
n_f <- length(heights_f)
n_m <- length(heights_m)
t <- (mean(heights_m) - mean(heights_f)) / (sd(singer_g$height) * 
        sqrt(1 / n_f + 1 / n_m))
t
#> [1] 11.2

Y rechazamos si \(t\) es menor/mayor al valor crítico \(t^*\).

t_star <- qt(0.025, n_h + n_m -2)
#> Error in qt(0.025, n_h + n_m - 2): object 'n_h' not found
t_star
#> Error in eval(expr, envir, enclos): object 't_star' not found

Datos nulos: ¿Cómo se ven los inocentes?

nulos <- data.frame(t = rt(10000, 233))
ggplot(nulos, aes(x = t)) +
    geom_histogram(color = "darkgray", fill = "darkgray") +
    geom_vline(xintercept = c(t_star, -t_star), color = "red", 
        alpha = 0.5) 
#> Error in data.frame(xintercept = xintercept): object 't_star' not found

¿Cómo calculamos el valor-p?

Inferencia visual

Los principios de pruebas de hipótesis son los mismos para pruebas visuales, a excepción de dos aspectos: la estadística de prueba y el mecanismo para medir similitud.

La estadística de prueba ahora es una gráfica de los datos, y en lugar de una diferencia matemática usamos el ojo humano.

En la siguiente prueba gráfica, los verdaderos datos están escondidos entre 19 gráficas de datos nulos, donde un dato nulo es una muestra de la distribución bajo la hipótesis nula. Si es posible identificar los datos, hay evidencia indicando que estos son distintos a los datos nulos.

Prueba visual 1. Genera n-1 datos nulos (datos que siguen la hipótesis nula)

2. Grafica los nulos + los datos reales, donde los datos están posicionados de manera aleatoria.

3. Muestra la gráfica a un observador imparcial.

¿Pueden distinguir los datos? Si es el caso, hay evidencia de diferencia verdadera (valor p = 1/n).

¿Porqué pruebas visuales?

En el ejemplo de estaturas se pueden utilizar pruebas estadísticas tradicionales, sin embargo, estas pruebas no cubren todas las complejidades que pueden surgir en una exploración de datos.

El siguiente es un lineup de nubes de palabras tomado de Graphical Inference for Infovis.

Regresando a estaturas

Volvamos al ejemplo de las estaturas, proponemos el siguiente modelo: la estatura es aproximadamente normal con media 179 para hombres y 164 para mujeres, la desviación estándar es de 6.5 en ambos casos.

singer_g %>% 
    group_by(gender) %>% 
    summarise(mean(height), sd(height))
#> # A tibble: 2 x 3
#>   gender `mean(height)` `sd(height)`
#>   <chr>           <dbl>        <dbl>
#> 1 F                164.         6.33
#> 2 M                179.         6.92

library(nullabor)
#> Error in library(nullabor): there is no package called 'nullabor'
singer_c <- singer_g %>%
    group_by(gender) %>%
    mutate(height_c = height - mean(height))
set.seed(26832)
sing_null_c <- lineup(null_dist('height_c', dist = 'normal', 
    params = list(mean = 0, sd = sd(singer_c$height_c))), n = 20, singer_c)
#> Error in lineup(null_dist("height_c", dist = "normal", params = list(mean = 0, : could not find function "lineup"
head(sing_null_c)
#> Error in head(sing_null_c): object 'sing_null_c' not found

Prueba:

ggplot(sing_null_c, aes(x = gender, y = height_c)) +
    facet_wrap(~ .sample) +
    geom_jitter(position = position_jitter(width = 0.1, height = 1), 
        size = 0.8, alpha = 0.5)
#> Error in ggplot(sing_null_c, aes(x = gender, y = height_c)): object 'sing_null_c' not found

El paquete nullabor

null_dist: Simula dada una distribución particular: Beta, Cauchy, Exponencial, Poisson,…

null_lm: Simula cuando la variable es una combinación lineal de predictores.

null_permute: Utiliza permutación, la variable es independiente de las otras.

Si se desea extender a otros modelos el artículo Supplementary Material for “Statistical Inference for Exploratory Data Analysis and Model Diagnostics” explica algunas consideraciones para generar datos nulos.

Diagramas de dispersión

Un diagrama de dispersión muestra la relación entre dos variables continuas y responde a la pregunta: ¿existe una relación entre \(x\) y \(y\)? Una posible hipótesis nula es que no hay relación entre las variables. Supongamos que queremos usar preubas visuales para esta hipótesis, la función null_permute del paquete nullabor recibe el nombre de una variable de los datos y la salida de la funcción consiste en la variable permutada para obtener los datos nulos.

En este ejercicio usarás los datos diamonds, toma una muestra de tamaño 5000 (sin reemplazo) y procede como se indica:

• Usa la función null_permute para crear una nueva base de datos con la variable depth permutada en los datos nulos.

• Usa la función line_up (como se usó en el caso de las estaturas) y genera una gráfica con 20 páneles, donde grafiques depth en el eje horizontal y carat en el eje vertical tienes evidencia para afirmar que existe una relación entre depth y carat.

• Explora ahora precio y carat.

Más allá que permutación

En muchos casos el supuesto de independencia es demasiado fuerte, es claro que las variables están relacionadas y queremos estudiar una relación particular. Por ejemplo, podemos pensar que los intentos de encestar a tres puntos en el basquetbol siguen una distribución cuadrática en el espacio: mientras el ángulo entre el jugador y la canasta aumenta el jugador se acerca más para asegurar el éxito. La siguiente figura prueba esta hipótesis usando datos de los tres punteros de los Lakers en la temporada 2008/2009, los datos se obtuvieron de Basketball Geek.

paths <- dir("data/2008-2009", pattern = "LAL", full.names = TRUE)

basket <- purrr::set_names(paths, paths) %>% 
    map_df(read_csv)

basket_LA <- basket %>%
  filter(team == "LAL", type == "3pt", !is.na(x), !is.na(y)) %>% # datos Lakers
  mutate(
    x = x + runif(length(x), -0.5, 0.5),
    y = y + runif(length(y), -0.5, 0.5),
    r = sqrt((x - 25) ^ 2 + y ^ 2),  # distancia a canasta
    angle = atan2(y, x - 25)) %>%  # ángulo
  filter(r > 20 & r < 39) %>% # lanzamientos en el rango típico
  dplyr::select(x, y, r, angle)

# guardar datos
write.table(basket_LA, file = "data/basket_LA.csv", sep = ",")

glimpse(basket_LA)
#> Observations: 1,411
#> Variables: 4
#> $ x     <dbl> 0.848, 41.391, 46.069, 36.613, 43.207, 7.706, 16.030, 1....
#> $ y     <dbl> 6.30, 26.07, 17.44, 29.61, 24.41, 27.99, 29.21, 4.84, 29...
#> $ r     <dbl> 25.0, 30.8, 27.4, 31.8, 30.5, 32.9, 30.6, 24.3, 33.6, 32...
#> $ angle <dbl> 2.887, 1.010, 0.691, 1.197, 0.930, 2.124, 1.869, 2.941, ...

basket_null <- lineup(null_lm(r ~ poly(angle, 2)), basket_LA, n = 10)
#> Error in lineup(null_lm(r ~ poly(angle, 2)), basket_LA, n = 10): could not find function "lineup"

ggplot(basket_null, aes(x = angle * 180 / pi, y = r)) +
    geom_point(alpha = 0.5, size = 0.8) +
    scale_x_continuous("Angle (degrees)", 
        breaks = c(0, 45, 90, 135, 180), 
    limits = c(0, 180)) +
    facet_wrap(~ .sample, nrow = 2)
#> Error in ggplot(basket_null, aes(x = angle * 180/pi, y = r)): object 'basket_null' not found

Los datos reales están escondidos entre un conjunto de datos nulos que siguen la hipótesis de una relación cuadrática, los conjuntos nulos se crean ajustando el modelo, produciendo predicciones y residuales y sumando los residuales rotados a las predicciones.

Otras consideraciones

Potencia

• La potencia en una prueba de hipótesis es la probabilidad de rechazar la hipótesis nula cuando esta es falsa.

• En el caso de pruebas visuales la potencia depende de la calidad de la gráfica.

• Se ha estudiado la potencia de las pruebas Validation of Visual Statistical Inference, Applied to Linear Models.

• El paquete nullabor incluye la función visual_power() para calcular el poder de una prueba simulada.

Valor p

• Si usamos un jurado compuesto por \(K\) jueces en lugar de un juez y \(k\) de ellos entonces el valor p combinado es \(P(X \le k)\) donde \(X\) tiene distribución \(Binomial(K, 1/20)\). Si todos los jueces identifican los datos el valor p sería \(0.05^K\)

• El paquete nullabor tiene una función para calcular el valor p de una prueba dada pvisual().

8.6.1 Cálculos de poder estadístico

Cuando se esta diseñando un estudio se determina la precisión en las inferencias que se desea, y esto determina el tamaño de muestra que se tomará. Usualmente se fija uno de los siguientes dos objetivos:

1. Se determina el error estándar de un parámetro o cantidad de interés. Por ejemplo, en encuestas electorales es típico reportar los resultados de esta encuesta más menos 3 puntos porcentuales tienen un nivel del 95% de confianza, cúantas personas se debe entrevistar para lograr esto?

2. Se determina la probabilidad de que un estadístico determinado sea estadísticamente significativo. Por ejemplo, cuando se hacen ensayos clínicos se determina un tamaño de muestra para que con probabilidad de x% se detecte una diferencia clinicamente relevante con el nuevo tratamiento (si es que este es efectivo).

En cualquiera de estos dos escenarios se necesita hacer supuestos para poder calcular el tamaño de muestra.

8.6.1.1 Tamaño de muestra para un error estándar determinado

Supongamos que queremos estimar el porcentaje de la población que apoya la pena de muerte. Sospechamos que la proporción es 60%, imaginemos que queremos una precisión (error estándar) de a lo más 0.05, o 5 puntos porcentuales. Bajo muestreo aleatorio simple, para una muestra de tamaño \(n\), el error estándar de la proporción \(p\) es \[\sqrt{p(1-p)/n}\] Sustituyendo nuestra expectativa \(p = 0.60\) llegamos a que el error estándar sería \(0.49/\sqrt{n}\), de tal manera que si queremos \(se(p) \le 0.05\) necesitamos \(n>96\), en el caso de proporciones es fácil determinar el tamaño de muestra de manera conservadora pues basta con suponer \(p = 0.5\).

se_fun_n <- function(n, p) sqrt(p * (1-p) / n)

xy <- data.frame(x = 20:220, y = seq(0, 1, 0.005))
ggplot(xy, aes(x = x, y = y)) +
    stat_function(fun = se_fun_n, args = list(p = 0.7), aes(color = "p=0.7")) +
    stat_function(fun = se_fun_n, args = list(p = 0.9), aes(color = "p=0.9")) +
    stat_function(fun = se_fun_n, args = list(p = 0.5), aes(color = "p=0.5")) +
    labs(x = "n", y = "se", color = "") +
    geom_segment(x = 20, xend = 100, y = 0.05, yend = 0.05, color = "red", 
        alpha = 0.3, linetype = "longdash") +
    geom_segment(x = 100, xend = 100, y = 0.05, yend = 0, color = "red", 
        alpha = 0.3, linetype = "longdash")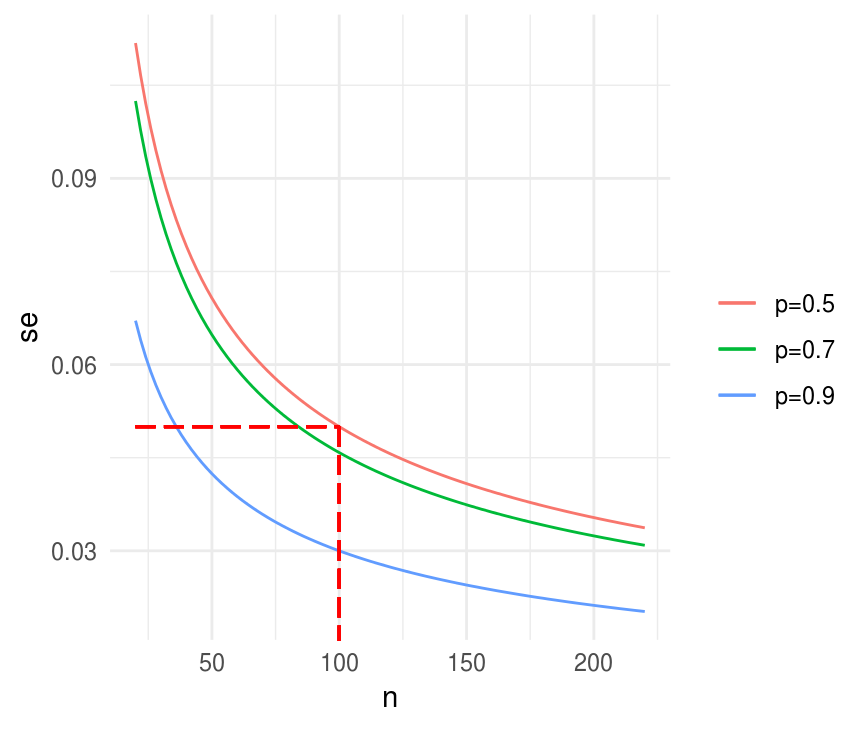

Cómo calcularíamos el tamaño de muestra simulando? Este caso es trivial calcular pero conforme se aumenta complejidad en el diseño de la muestra o en el estadístico de interés también se complica encontrar una solución analítica.

sim_p_hat <- function(n, p, n_sims = 1000){
    sim_muestra <- rbinom(n_sims, size = n, prob = p)
    se_p_hat <- sd(sim_muestra / n)
    data_frame(n = n, se_p_hat = se_p_hat, p = p)
}

sims_.7 <- map_df(seq(20, 220, 10), ~sim_p_hat(n = ., p = 0.7))
sims_.5 <- map_df(seq(20, 220, 10), ~sim_p_hat(n = ., p = 0.5))
sims_.9 <- map_df(seq(20, 220, 10), ~sim_p_hat(n = ., p = 0.9))
sims <- bind_rows(sims_.7, sims_.5, sims_.9)

ggplot(sims, aes(x = n, y = se_p_hat, color = factor(p), group = p)) +
    geom_smooth(se = FALSE, size = 0.5) +
    labs(x = "n", y = "se", color = "") +
    geom_segment(x = 20, xend = 100, y = 0.05, yend = 0.05, color = "red", 
        alpha = 0.3, linetype = "longdash") +
    geom_segment(x = 100, xend = 100, y = 0.05, yend = 0, color = "red", 
        alpha = 0.3, linetype = "longdash")
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'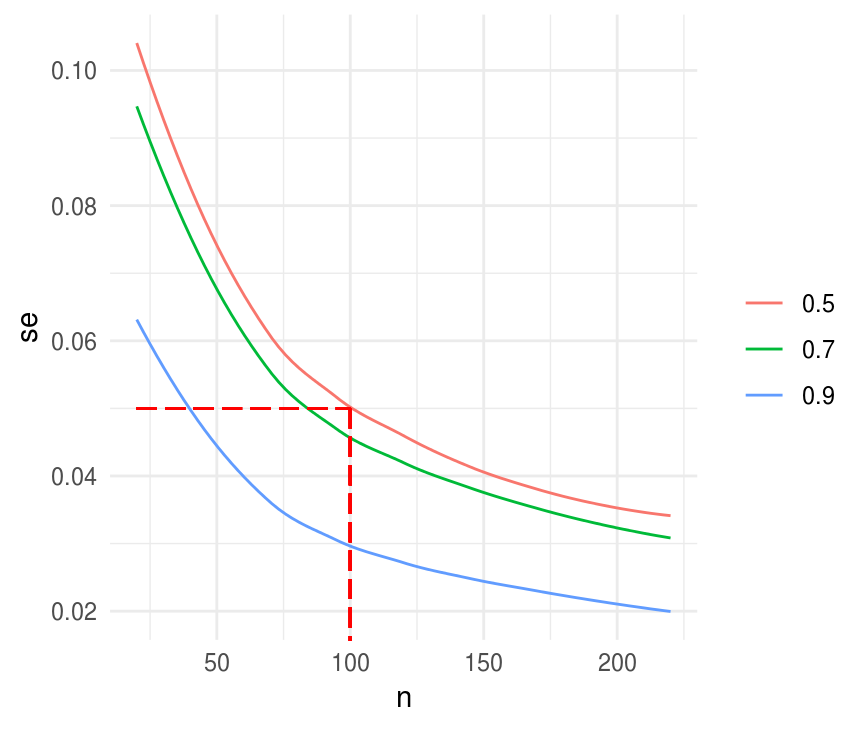

8.6.1.2 Tamaño de muestra determinado para obtener significancia estadística con una probabilidad determinada

Supongamos que nuestro objetivo es demostrar que más de la mitad de la población apoya la pena de muerte, esto es \(p>0.5\), nuevamente tenemos la hipótesis que el verdadero valor es \(p=0.6\).

Un prueba de potencia típica tiene un poder de 80%, es decir nos gustaría seleccionar \(n\) tal que 80% de los intervalos construidos con 95% de confianza no incluyan 0.5. Para encontrar la \(n\) tal que el 80% de las estimaciones estén al menos, 1.96 errores estándar por encima de 0.5 necesitamos que:

\[0.5 + 1.96 se = 0.6 - 0.84 se\]

Sustituyendo \(se = 0.5/\sqrt(n)\) obtenemos \(n=196\)

Y simulando sería

sim_potencia <- function(n, p, n_sims = 1000){
    sim_muestra <- rbinom(n_sims, size = n, prob = p)
    se_p_hat <- sd(sim_muestra / n)
    acepta <- (sim_muestra / n - 1.96 * se_p_hat) > 0.5
    data_frame(n = n, potencia = mean(acepta))
}
sims <- map_df(c(2, 10, 50, 80, 100, 150, 200, 300, 500), ~sim_potencia(n = ., p = 0.6))

ggplot(sims) +
    geom_line(aes(x = n, y = potencia)) +
    geom_hline(yintercept = 0.8, color = "red", alpha = 0.5)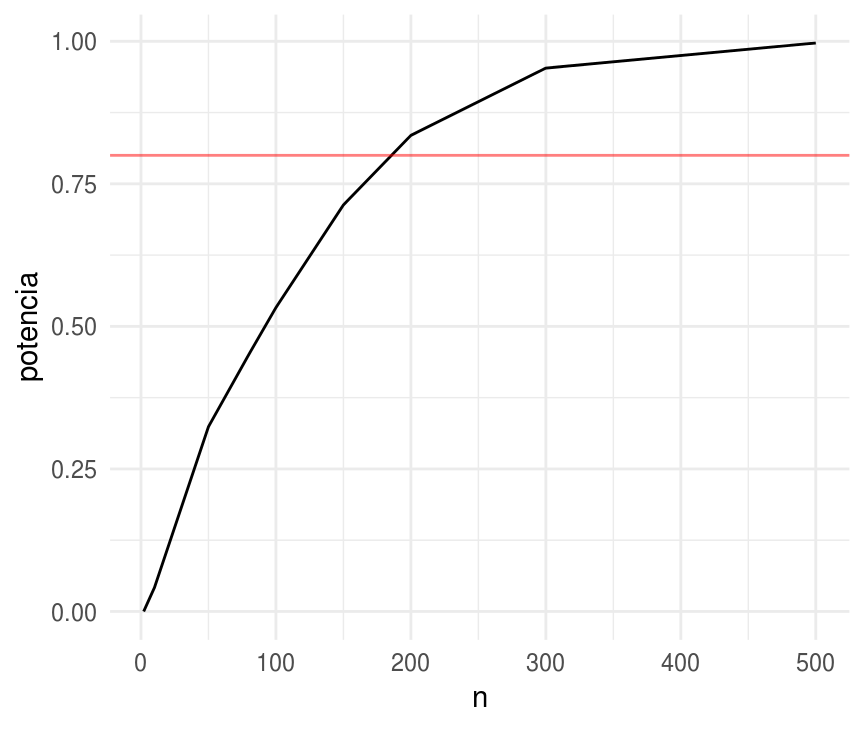

Veamos un ejemplo más interesante, tenemos medidas del sistema inmune (porcentaje de CD4 en transformado con raíz cuadrada) de niños VIH positivos a lo largo de un periodo de 2 años. Las series de tiempo se ajustan de manera razonable con un modelo de intercepto y pendiente variable:

\[y_i \sim N(\alpha_{j[i]} + \beta_{j[i]}t_i, \sigma^2_y)\] donde \(i\) indexa las mediciones tomadas al tiempo \(i\) en el individuo \(j[i]\).

# preparación de los datos
library(lme4)
allvar <- read.csv("data/allvar.csv")
cd4 <- allvar %>% 
    filter(treatmnt == 1, !is.na(CD4PCT), baseage > 1, baseage < 5) %>% 
    mutate(
        y = sqrt(CD4PCT), 
        person = newpid, 
        time = visage - baseage
        ) 

La siguiente gráfica muestra las mediciones para cada individuo, podemos ver que las series de tiempo son ruidosas.

ggplot(cd4, aes(x = time, y = y, group = person)) +
    geom_line(alpha = 0.5)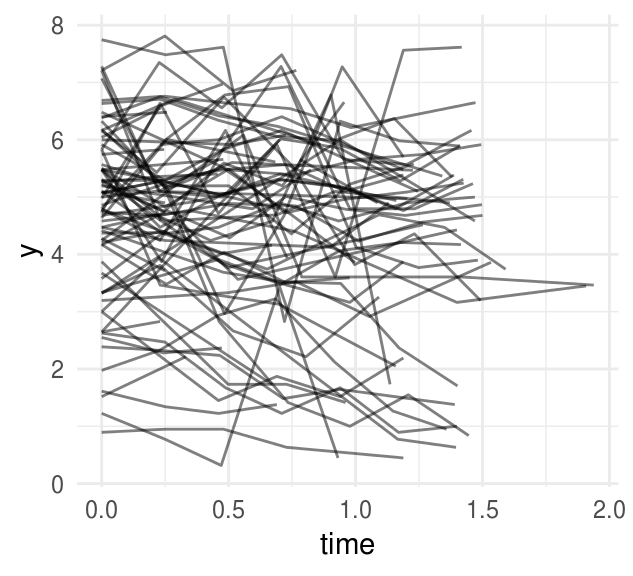

Veamos un ajuste usando la función lmer() del paquete lme4.

fit_cd4 <- lmer(formula = y ~ time + (1 + time | person), cd4)
fit_cd4
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: y ~ time + (1 + time | person)
#>    Data: cd4
#> REML criterion at convergence: 1096
#> Random effects:
#>  Groups   Name        Std.Dev. Corr
#>  person   (Intercept) 1.329        
#>           time        0.680    0.15
#>  Residual             0.748        
#> Number of obs: 369, groups:  person, 83
#> Fixed Effects:
#> (Intercept)         time  
#>       4.846       -0.468

Notamos que las tendencias sobre el tiempo \(\beta\) tienen un promedio estimado en -0.5 con desviación estándar de 0.7, es decir, estimamos que la mayoría de los niños tienen niveles de CD4 decrecientes, pero no todos.

Usaremos estos resultados para hacer calculos de potencia para una nueva prueba que busca medir el efecto del consumo de zinc en la dieta. Quisiéramos que el estudio fuera suficientemente grande para que con probabilidad de al menos 80% la media del efecto del tratamiento sea significativo con un nivel de confianza del 95%.

Necesitamos hacer supuestos del efecto del tratamiento y del resto de los parámetros que caracterizan el estudio. El análisis de arriba muestra que en los niños VIH positivos que no recibieron zinc los niveles de CD4 caían en promedio 0.5 al año. Suponemos que con el zinc reduciremos la caída a cero.

\[ y_i \sim N(\alpha_{j[i]} + \beta_{j[i]}t_i, \sigma^2_y) \]

\[ \begin{eqnarray*} \begin{pmatrix}\alpha_{j}\\ \beta_{j} \end{pmatrix} & \sim & N\left[\left(\begin{array}{c} \gamma_0^{\alpha}\\ \gamma_0^{\beta}+\gamma_1^{\beta}z_j \end{array}\right), \left(\begin{array}{cc} \sigma^2_{\alpha} & \rho \sigma_{\alpha}\sigma_{\beta}\\ \rho \sigma_{\alpha}\sigma_{\beta} & \sigma^2_{\beta} \end{array}\right)\right] \end{eqnarray*} \] donde

\[ z_j = \left\{ \begin{array}{lr} 1 & \text{si el }j \text{-ésimo niño recibió trataiento}\\ 0 & e.o.c \end{array} \right. \]

El tratamiento \(z_j\) afecta la pendiente \(\beta_j\) más no el intercepto \(\alpha_j\) pues el tratamiento no puede afectar en el tiempo cero. Usando los datos del ajuste de arriba tenemos que para el grupo control la pendiente será

\(\gamma_0^{\beta} = -0.5\) y el efecto del tratamiento \(\gamma_1^{\beta} = 0.5\), el resto de los parámetros los especificamos de acuerdo al ajuste de arriba. Por simplicidad fijaremos la correlación \(\rho\) en cero.

El siguiente paso es determinar el diseño del modelo, suponemos que dividiremos a \(J\) niños VIH positivos en dos grupos del mismo tamaño, \(J/2\) de ellos recibirán el cuidado usual y \(J/2\) recibirán suplementos de zinc. Más aún suponemos que se medirá el porcentaje de CD4 cada 2 meses durante un año.

Usaremos simulación para determinar el tamaño de muestra \(J\) que se requiere para tener una potencia de \(80%\) si el verdadero efecto es 0.5, ¿cuál es el modelo gráfico asociado?

# cd4_sim simula del modelo con los supuestos que fijamos arriba
#   podemos variar los valores de los parámetros para cambiar el escenario
cd4_sim <- function (J, K, mu.a.true = 4.8, g.0.true = -0.5, g.1.true = 0.5, 
    sigma.y.true = 0.7, sigma.a.true = 1.3, sigma.b.true = 0.7){
    time <- rep(seq(0, 1, length = K), J) # K mediciones en el año
    person <- rep (1:J, each = K)        # ids
    treatment <- sample(rep(0:1, J/2))
    treatment1 <- treatment[person]
    # parámetros a nivel persona
    a.true <- rnorm(J, mu.a.true, sigma.a.true)
    b.true <- rnorm(J, g.0.true + g.1.true * treatment, sigma.b.true)
    y <- rnorm (J * K, a.true[person] + b.true[person] * time, sigma.y.true)
    return (data.frame(y, time, person, treatment1))
}

# calcular si el parámetro es significativo para una generación de simulación
cd4_signif <- function (J, K){
    fake <- cd4_sim(J, K)
    lme_power <- lmer (y ~ time + time:treatment1 + (1 + time | person), data = fake)
    theta_hat <- fixef(lme_power)["time:treatment1"]
    theta_se <- summary(lme_power)$coefficients["time:treatment1", "Std. Error"]
    theta_hat - 1.96 * theta_se > 0
}

# repetir la simulación de cd4 n_sims veces y calcular el porcntaje de las
#   muestras en que es significativo el parámetro (el poder)
cd4_power <- function(n_sims, J, K){
    rerun(n_sims, cd4_signif(J, K = 7)) %>% flatten_dbl() %>% mean()
}

# calculamos el poder para distintos tamaños de muestra, con 7 mediciones al año
potencias <- map_df(c(8, 16, 60, 100, 150, 200, 225, 250, 300, 400), 
    ~data_frame(n = ., p = cd4_power(n_sims = 500, J = ., K = 7)))
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control
#> $checkConv, : unable to evaluate scaled gradient
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control
#> $checkConv, : Model failed to converge: degenerate Hessian with 1 negative
#> eigenvalues
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control
#> $checkConv, : unable to evaluate scaled gradient
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control
#> $checkConv, : Model failed to converge: degenerate Hessian with 1 negative
#> eigenvalues
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control
#> $checkConv, : unable to evaluate scaled gradient
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control
#> $checkConv, : Model failed to converge: degenerate Hessian with 1 negative
#> eigenvalues

ggplot(potencias, aes(x = n, y = p)) +
    geom_hline(yintercept = 0.8, color = "red", alpha = 0.5) +
    geom_line()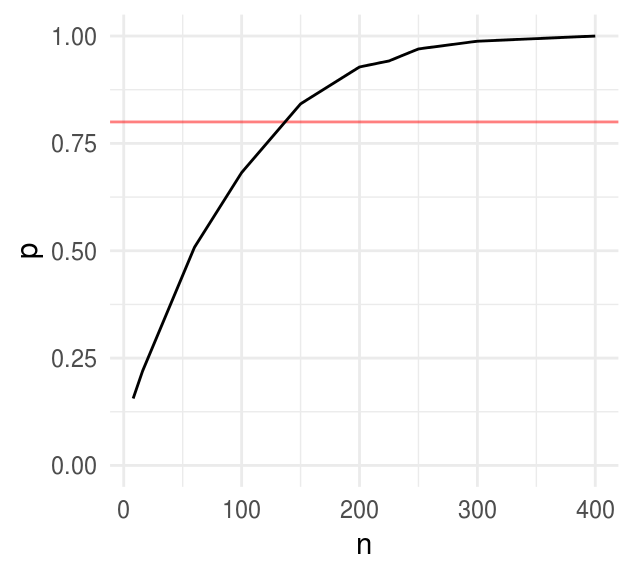

Notemos que la función cd4_rep() regresa la proporción de las simulaciones en las que el resultado es estadísticamente significarivo, est es, la potencia calculada con simulaicón, para un estudio con \(J\) niños medidos en \(K\) intervalos igualmente espaciados.

Notemos también que en el límite, cuando \(J \to 0\) el poder es 0.025, esto es, con una muestra suficientemente chica el efecto del estimador es básicamente aleatorio y por tanto en 2.5% de los casos el estimador está 2 desviaciones por encima de cero.

Una ventaja de usar simulación para calcular potencia es que nos permite flexibilidad, por ejemplo, es fácil calcular para más escenarios:

• ¿qué ocurriría si solo puedo medir 3 veces al año?

• Se sabe que es común que algunos participantes abandonen el estudio, o no asistan a todas las mediciones, con simulación es fácil incorporar faltantes.

8.6.2 ¿Para qué simular?

• Alternativa para presentar inferencias: en lugar de presentar un estimador puntual y/o intervalo de confianza podemos analizar simulaciones del modelo.

• Inferencia predictiva: es fácil usar simulación para calcular errores estándar, o intervalos de confianza, resulta particularmente útil cuando estamos estimando cantidades que no son coeficientes de un modelo o transformaciones lineales de coeficientes.

• Simulación para revisar el ajuste de un modelo. Podemos simular datos del modelo ajustado y compararlos con los datos verdaderos.