8.2 Modelos gráficos y simulación predictiva

El objetivo de esta sección es la simulación de modelos, una manera conveniente de simular de un modelo probabilístico es a partir del modelo gráfico asociado. Un modelo gráfico representa todas las cantidades involucradas en el modelo mediante nodos de una gráfica dirigida, el modelo representa el supuesto que dados los nodos padres \(padres(v)\) cada nodo es independiente del resto de los nodos a excepción de sus descendientes.

Los nodos en las gráficas se clasifican en 3 tipos:

  • Constantes fijas por el diseño del estudio, siempre son nodos sin padres.

  • Estocásticos son variables a los que se les asigna una distribución.

  • Determinísticos son funciones lógicas de otros nodos.

Los supuestos de independencia condicional que representa la gráfica implican que la distribución conjunta de todas las cantidades V tiene una factorización en términos de la distribución condicional \(p(v|padres(v))\) de tal manera que: \[p(V) = \prod p(v|padres(v))\]

Veamos como usar las gráficas para simular de modelos probabilísticos. Los siguientes ejemplos están escritos con base en Gelman and Hill (2007).

Ejemplo de simulación discreta predictiva

La probabilidad de que un bebé sea niña o niño es \(48.8\%\) y \(51.2\%\) respectivamente. Supongamos que hay 400 nacimientos en un hospital en un año dado. ¿Cuántas niñas nacerán?

Comencemos viendo el modelo gráfico asociado.

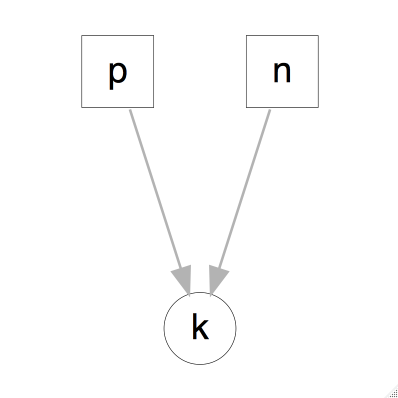
La gráfica superior muestra todas las variables relevantes en el problema, y las dependencias entre ellas. En este caso \(n\) es una constante que representa el número de nacimientos, (\(n=400\)), \(p=48.8\) es la probabilidad de que un nacimiento resulte en niña y \(k \sim Binomial(p, n)\). Debido a que el número de éxitos (nacimientos que resultan en niña) depende de la tasa \(p\) y el número de experimentos \(n\), los nodos que representan a éstas dos últimas variables están dirigidos al nodo que representa \(k\).

Una vez que tenemos la gráfica es fácil simular del modelo:

library(ggplot2)
library(dplyr)
library(arm)
library(tidyr)
set.seed(918739837)
n_ninas <- rbinom(1, 400, 0.488)

esto nos muestra algo que podría ocurrir en \(400\) nacimientos. Ahora, para tener una noción de la distribución simulamos el proceso \(1000\) veces:

sims_ninas <- rerun(1000, rbinom(1, 400, 0.488)) %>% flatten_dbl()
mean(sims_ninas)
#> [1] 196
sd(sims_ninas)
#> [1] 10.1

ggplot() + geom_histogram(aes(x = sims_ninas), binwidth = 3, alpha = 0.7)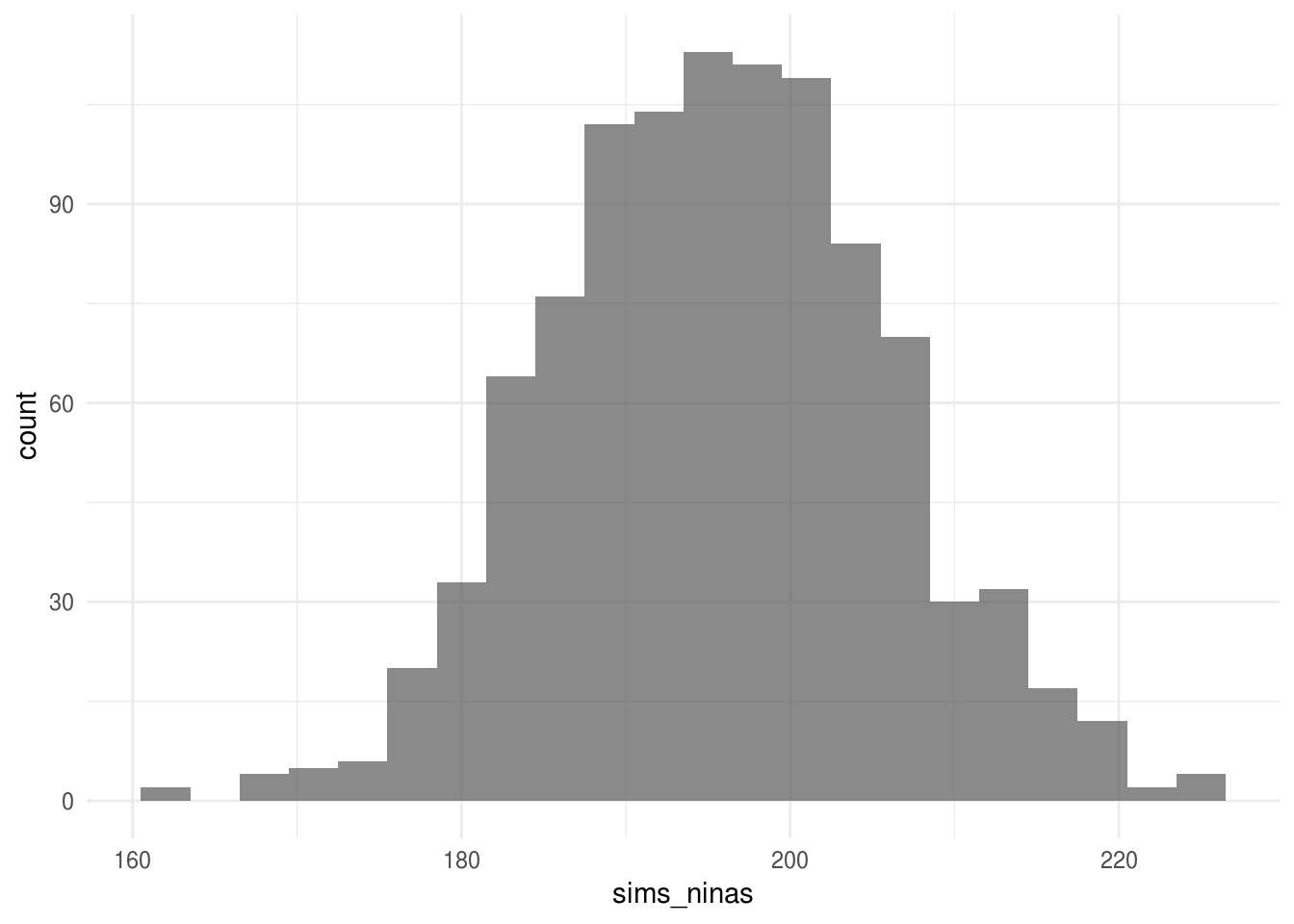

El histograma de arriba representa la distribución de probabilidad para el número de niñas y refleja la incertidumbre en los nacimientos.

Podemos agregar complejidad al modelo, por ejemplo con probabilidad \(1/125\) un nacimiento resulta en gemelos fraternales, y para cada uno de los bebés hay una posibilidad de aproximadamente \(49.5\%\) de ser niña. Además la probabilidad de gemelos idénticos es de \(1/300\) y estos a su vez resultan en niñas en aproximadamente \(40.5\%\) de los casos.

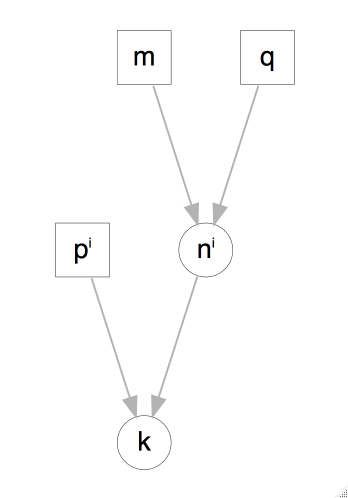
Podemos simular 400 nacimientos bajo este modelo como sigue:

tipo_nacimiento <- sample(c("unico", "fraternal", "identicos"), 
  size = 400, replace = TRUE, prob = c(1 - 1 / 125 - 1 / 300, 1 / 125, 1 / 300))
n_unico <- sum(tipo_nacimiento == "unico")  # número de nacimientos únicos
n_fraternal <- sum(tipo_nacimiento == "fraternal")
n_identicos <- 400 - n_unico - n_fraternal
n_ninas <- rbinom(1, n_unico, 0.488) +
           rbinom(1, 2 * n_fraternal, 0.495) + # en cada nacimiento hay 2 bebés
           2 * rbinom(1, n_identicos, 0.405)
n_ninas
#> [1] 183

Repetimos la simulación 1000 veces para aproximar la distribución de número de niñas en 400 nacimientos.

modelo2 <- function(){
    tipo_nacimiento <- sample(c("unico", "fraternal", "identicos"), 
        size = 400, replace = TRUE, prob = c(1 - 1 / 125 - 1 / 300, 1 / 125, 1 / 300))
    # número de nacimientos de cada tipo
    n_unico <- sum(tipo_nacimiento == "unico")  # número de nacimientos únicos
    n_fraternal <- sum(tipo_nacimiento == "fraternal")
    n_identicos <- 400 - n_unico - n_fraternal
    # simulamos para cada tipo de nacimiento
    n_ninas <- rbinom(1, n_unico, 0.488) +
        rbinom(1, 2 * n_fraternal, 0.495) + # en cada nacimiento hay 2 bebés
    2 * rbinom(1, n_identicos, 0.405)
  n_ninas
}

sims_ninas_2 <- rerun(1000, modelo2()) %>% flatten_dbl()
mean(sims_ninas_2)
#> [1] 198
sd(sims_ninas_2)
#> [1] 10.2
ggplot() + geom_histogram(aes(x = sims_ninas_2), binwidth = 4, alpha = 0.7)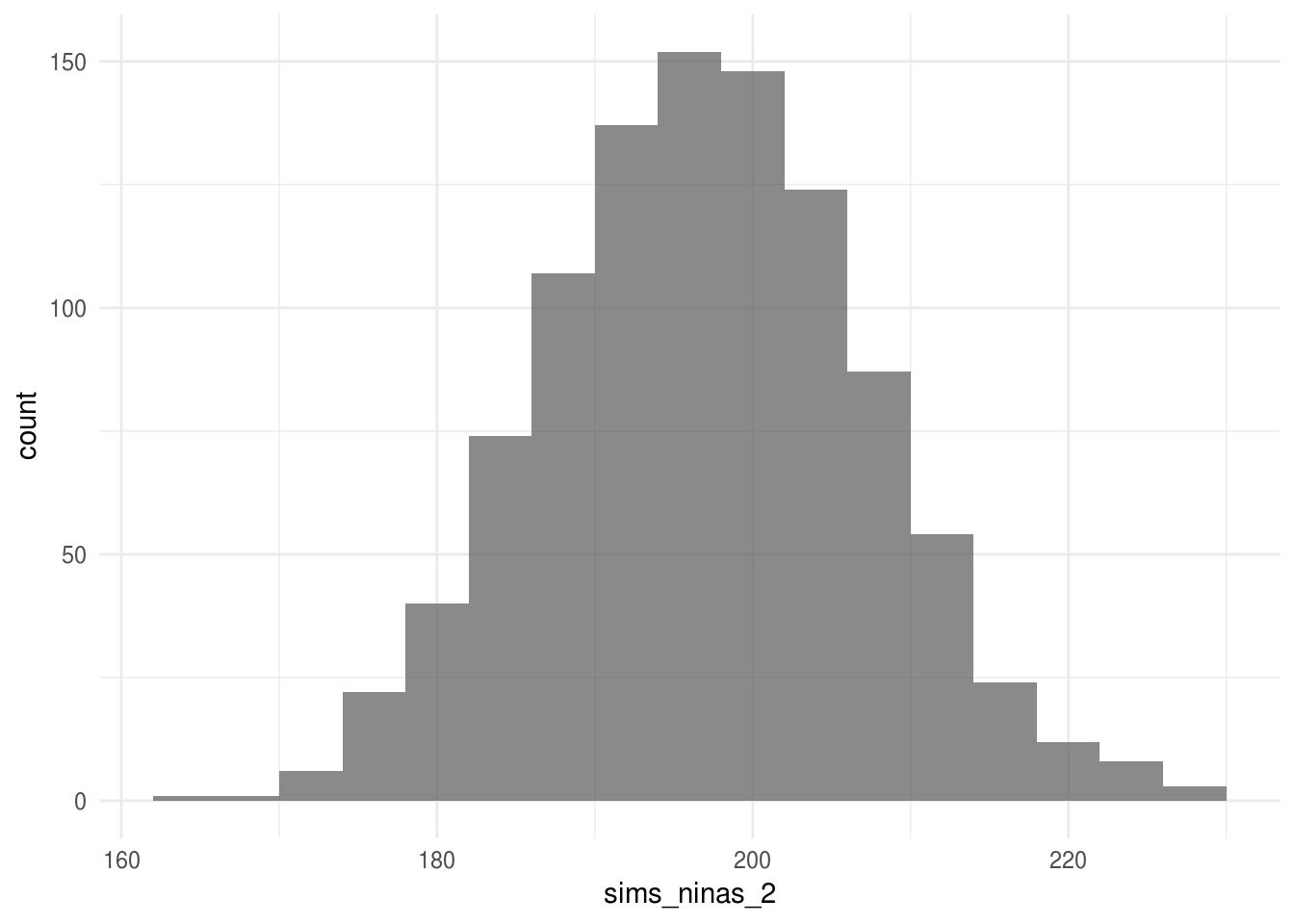

8.2.0.1 Ejemplo de simulación continua predictiva

El 52% de los adultos en EUA son mujeres y el 48% hombres, las estaturas de los hombres se distribuyen aproximadamente normal con media 175 cm y desviación estándar de 7.37 cm, en el caso de las mujeres la distribución es aproximadamente normal con media 161.80 cm y desviación estándar de 6.86 cm. Supongamos que seleccionamos 10 adultos al azar, ¿cuál es el modelo gráfico asociado? ¿qué podemos decir del promedio de estatura?

sexo <- rbinom(10, 1, 0.52)
altura <- rnorm(sexo, mean = 161.8 * (sexo == 1) + 175 * (sexo == 0), 
  sd = 6.86 * (sexo == 1) + 7.37 * (sexo == 0))
mean(altura)
#> [1] 172

Simulamos la distribución de la altura promedio:

mediaAltura <- function(){
  sexo <- rbinom(10, 1, 0.52)
  altura <- rnorm(sexo, mean = 161.8 * (sexo == 1) + 175 * (sexo == 0), 
    sd = 6.86 * (sexo == 1) + 7.37 * (sexo == 0))
}
sims_alturas <- rerun(1000, mediaAltura()) 
media_alturas <- sims_alturas %>% map_dbl(mean)
mean(media_alturas)
#> [1] 168
sd(media_alturas)
#> [1] 3.05
ggplot() + geom_histogram(aes(x = media_alturas), binwidth = 1.2, alpha = 0.7)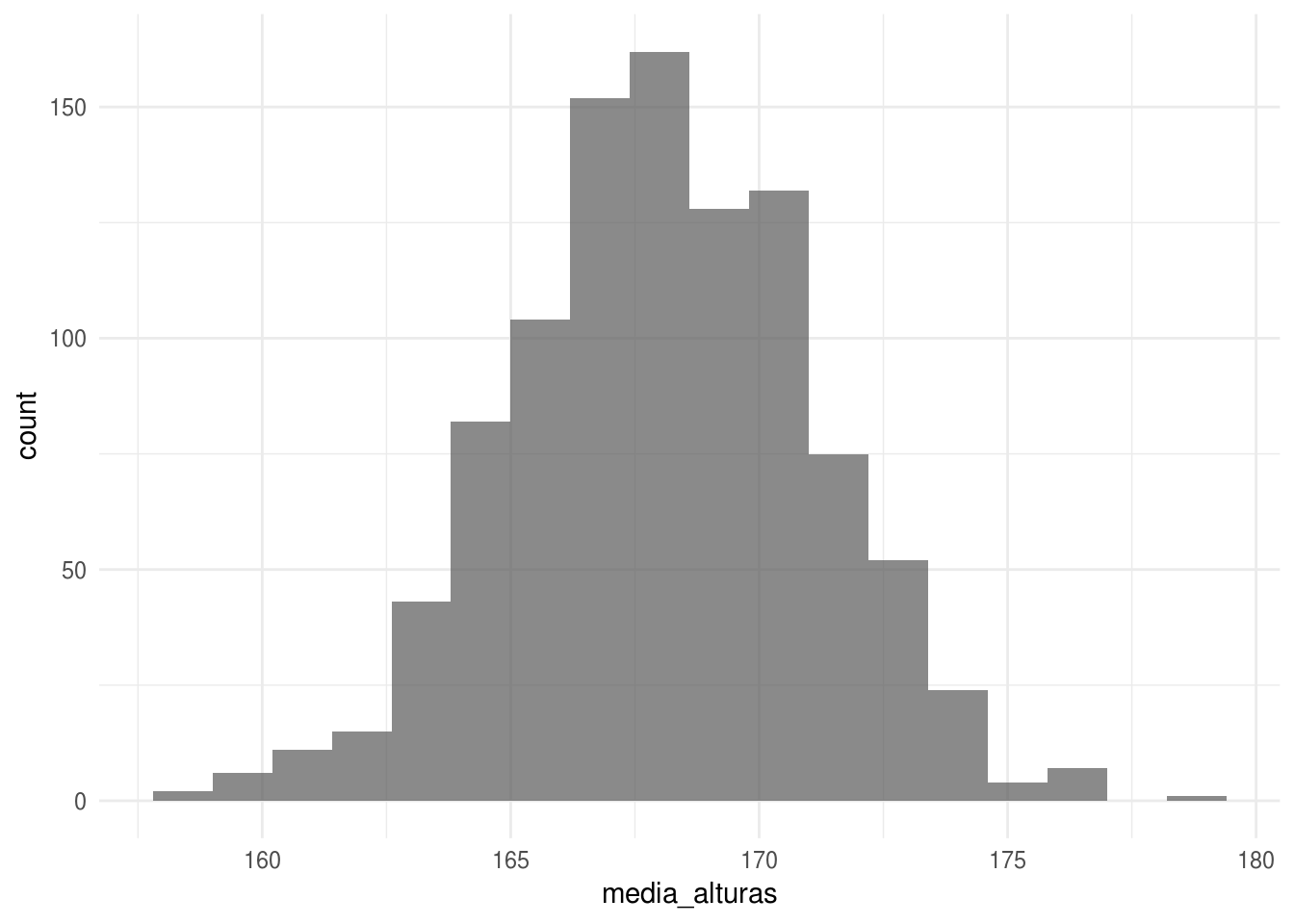

¿Y que podemos decir de la altura máxima?

alt_max <- sims_alturas %>% map_dbl(max)
qplot(alt_max, geom = "histogram", binwidth = 1.5)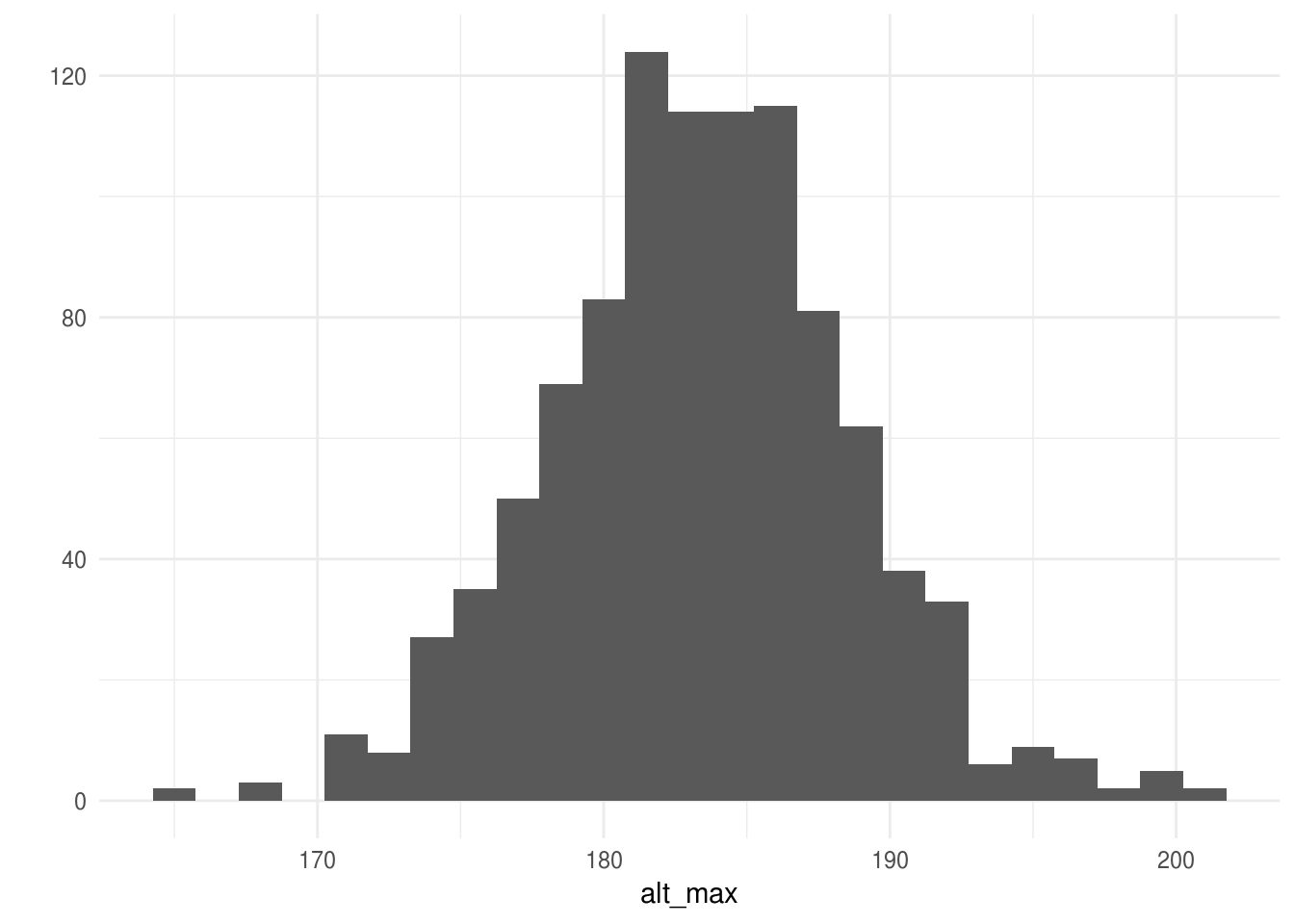

Supongamos que una compañía cambia la tecnología usada para producir una cámara, un estudio estima que el ahorro en la producción es de $5 por unidad con un error estándar de $4. Más aún, una proyección estima que el tamaño del mercado (esto es, el número de cámaras que se venderá) es de 40,000 con un error estándar de 10,000. Suponiendo que las dos fuentes de incertidumbre son independientes, usa simulación de variables aleatorias normales para estimar el total de dinero que ahorrará la compañía, calcula un intervalo de confianza.

8.2.0.2 Ejemplo de simulación de un modelo de regresión

En regresión utilizamos simulación para capturar tanto la incertidumbre en la predicción (término de error en el modelo) como la incertidumbre en la inferencia (errores estándar de los coeficientes e incertidumbre del error residual).

Comenzamos con un ejemplo en el que simulamos únicamente incertidumbre en la predicción.

Supongamos que el puntaje de un niño de tres años en una prueba cognitiva esta relacionado con las características de la madre, el siguiente modelo resume la diferencia en los puntajes promedio de los niños cuyas madres se graduaron de preparatoria y los que no.

\[y_i= \beta_0 + \beta_1 X_{i1} + \epsilon_i\]

  • donde \(y_i\) es el puntaje del \(i\)-ésimo niño,
  • \(X_{i1}\) es una variable binaria que indica si la madre se graduó de preparatoria (codificado como \(1\)) o no (codificado como \(0\)), y
  • \(\epsilon_i\) son los error aleatorios, estos son independientes con distribución normal \(\epsilon_i \sim N(0, \sigma^2)\).

Ahora consideremos el problema de simular el puntaje de \(50\) niños \(30\) con madres que terminaron la preparatoria y \(20\) cuyas madres no terminaron. Los coeficientes que usaremos son:

\[\beta_0 = 78\] \[\beta_1 = 12\] \[\sigma = 20\]

El modelo gráfico asociado sería como sigue:

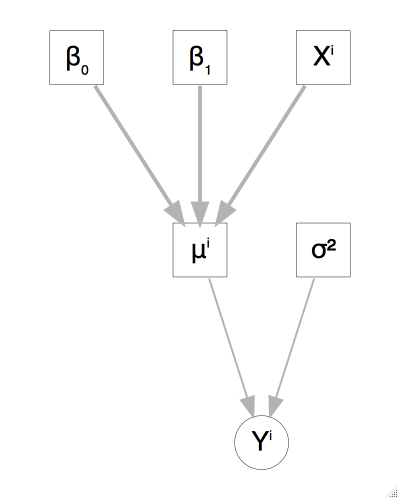
vector_mu <- c(rep(78 + 12, 30), rep(78, 20)) # beta_0 + beta_1 X
y <- rnorm(50, vector_mu, 20)
sims_y <- rerun(2000, rnorm(50, vector_mu, 20))

Podemos calcular la media y su intervalo de confianza:

medias <- sims_y %>% map_dbl(mean)
quantile(medias, c(0.025, 0.975))
#>  2.5% 97.5% 
#>  79.7  90.8

qplot(medias, geom = "histogram", binwidth = 1.5)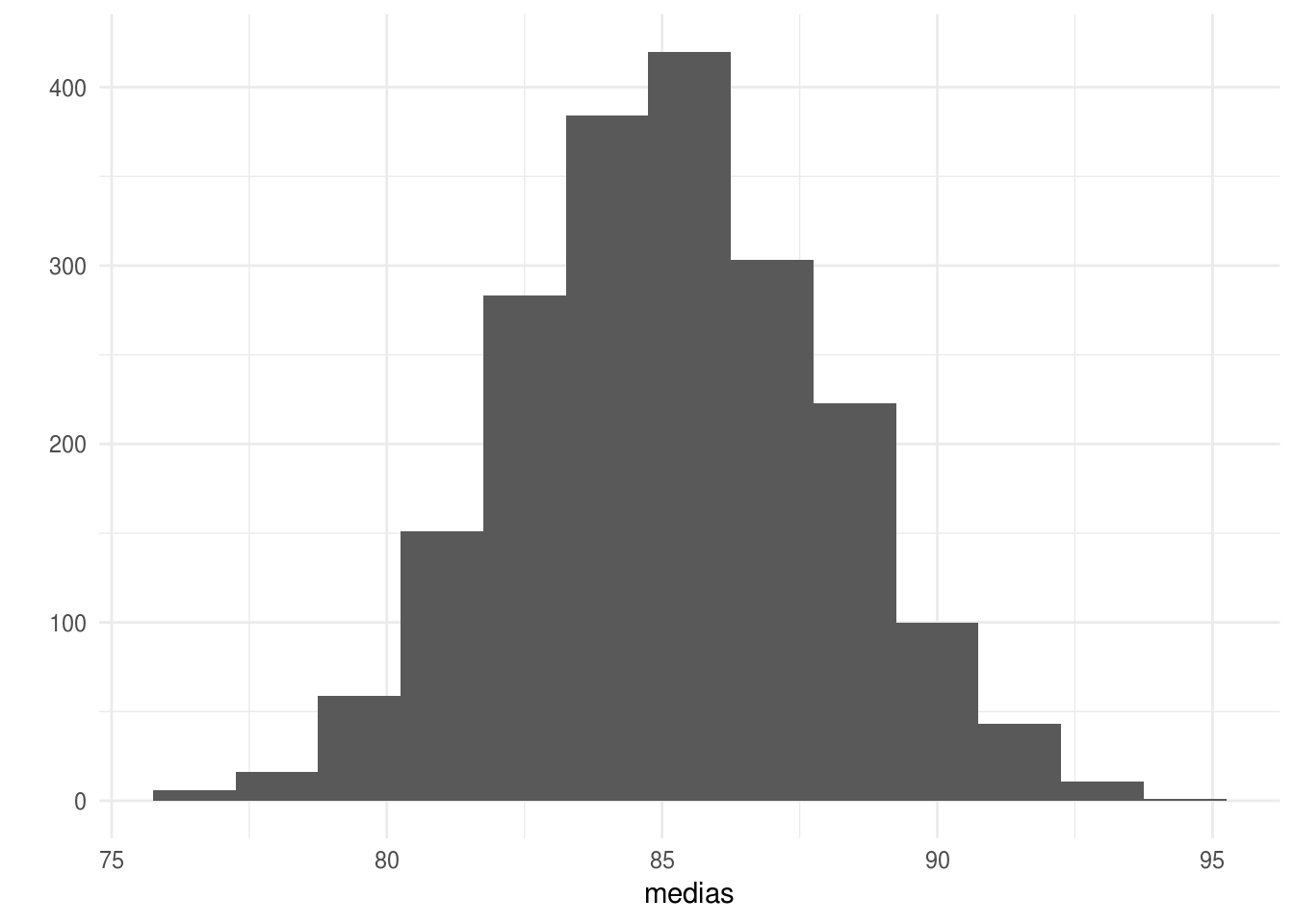

Supongamos ahora que nos interesa incorporar que tenemos incertidumbre en los coeficientes de regresión, y expresamos nuestra incertidumbre a través de distribuciones de probabilidad, ¿cómo sería el modelo gráfico asociado?

Primero suponemos que \(\sigma^2\) tiene una distribución centrada en \(20^2\), proporcional a una distribución \(\chi^2\) con \(432\) grados de libertad.

\[ \begin{eqnarray*} \begin{pmatrix}\beta_{0}\\ \beta_{1} \end{pmatrix} & \sim & N\left[\left(\begin{array}{c} 78\\ 12 \end{array}\right), \sigma^2 \left(\begin{array}{cc} 0.01 & -0.01\\ -0.01 & 0.01 \end{array}\right)\right] \end{eqnarray*} \]

Finalmente, simulamos del modelo incorporando tanto la incertidumbre correpondiente a la predicción como la incertidumbre en los coeficientes de regresión.

  1. Simula \(\sigma=20\sqrt{(432)/X}\) donde \(X\) es una generación de una distribución \(\chi^2\) con \(432\) grados de libertad.

  2. Dado \(\sigma\) (obtenido del paso anterior), simula \(\beta\) de una distribución normal multivariada con media \((77,12)\) y matriz de covarianzas \(\sigma^2 V\).

  3. Simula \(y\) el vector de observaciones usando los parámetros de \(1\) y \(2\).

simula_parametros <- function(){
    # empezamos simulando sigma
    sigma <- 20 * sqrt((432) / rchisq(1, 432))
    # la usamos para simular betas
    beta <- MASS::mvrnorm(1, mu = c(78, 12), 
        # Sigma = sigma ^ 2 * matrix(c(4.2, -4.2, -4.2, 5.4), nrow = 2))
        Sigma = sigma ^ 2 * matrix(c(0.011, -0.011, -0.011, 0.013), nrow = 2))
    # Simulamos parámetros
    list(sigma = sigma, beta = beta)
}

sims_parametros <- rerun(10000, simula_parametros()) 

# simulamos los puntajes
simula_puntajes <- function(beta, sigma, n_hs = 30, n_nhs = 20){
    vector_mu <- c(rep(beta[1] + beta[2], n_hs), rep(beta[1], n_nhs)) # beta_0 + beta_1 X
    obs = rnorm(50, vector_mu, sigma)
}

sims_puntajes <- map(sims_parametros, ~simula_puntajes(beta = .[["beta"]], sigma = .[["sigma"]]))
medias_incert <- sims_puntajes %>% map_dbl(mean)

quantile(medias_incert, c(0.025, 0.975))
#>  2.5% 97.5% 
#>  79.2  90.9
qplot(medias_incert, geom = "histogram", binwidth = 1)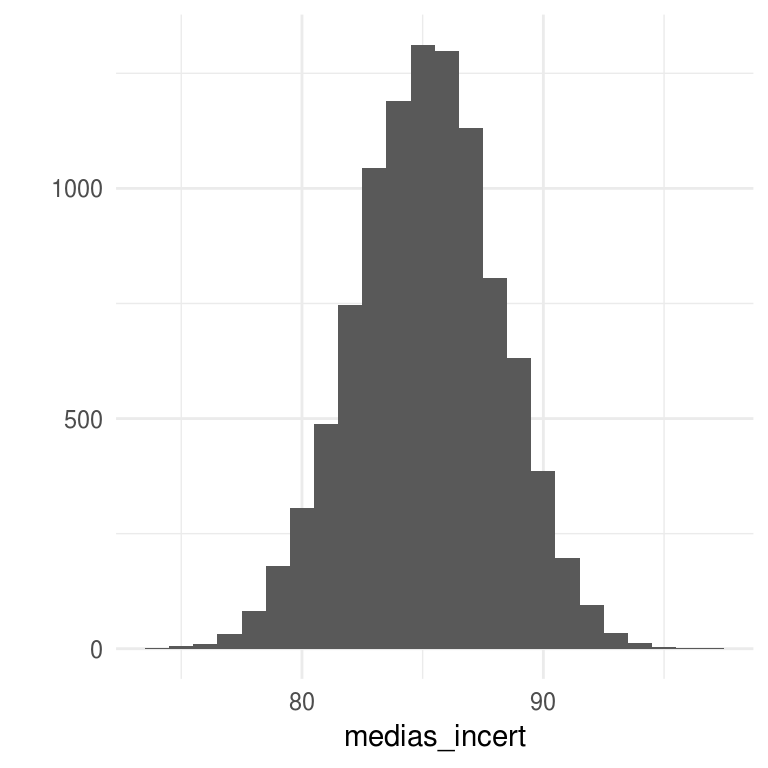

Los parametros se obtuvieron de ajustar el modelo de regresión lineal.

library(foreign)
kids_iq <- read.dta("data/kidiq.dta")
lm_kid <- lm(kid_score ~ mom_hs, kids_iq)
V <- vcov(lm_kid) / 20 ^ 2
summary(lm_kid)
#> 
#> Call:
#> lm(formula = kid_score ~ mom_hs, data = kids_iq)
#> 
#> Residuals:
#>    Min     1Q Median     3Q    Max 
#> -57.55 -13.32   2.68  14.68  58.45 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)    77.55       2.06   37.67   <2e-16 ***
#> mom_hs         11.77       2.32    5.07    6e-07 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 19.9 on 432 degrees of freedom
#> Multiple R-squared:  0.0561, Adjusted R-squared:  0.0539 
#> F-statistic: 25.7 on 1 and 432 DF,  p-value: 5.96e-07

Podemos usar simulación para calcular intervalos de confianza para \(\beta_0\) y \(\beta_1\),

sims_parametros %>% map_dbl(~(.$beta[1])) %>% sd()
#> [1] 2.11
sims_parametros %>% map_dbl(~(.$beta[2])) %>% sd()
#> [1] 2.3

No parece que valga la pena el esfuerzo cuando podemos calcular los intervalos analíticamente, sin embargo con simulación podemos responder fácilmente otras preguntas, por ejemplo, la pregunta inicial: ¿cuál es la media esperada para un conjunto de \(50\) niños, \(30\) con madres que hicieron preparatoria y \(20\) que no? es fácil de responder con simulación.

Podríamos usar predict() para calcular el estimador puntual de la media en el examen para los niños:

pred_mi_pob <- predict(lm_kid, newdata = data.frame(mom_hs = c(rep(1, 30), 
    rep(0, 20))), se.fit = TRUE)
mean(pred_mi_pob$fit)
#> [1] 84.6

¿Cómo calculas el error estándar? En este caso se puede resolver pues es una combinación lineal de los coeficientes del modelo, pero en muchos casos nuestro objetivo es más complicado que coeficientes o combinaciones lineales de estos.

8.2.0.3 Simulación de predicciones no lineales

Veamos un ejemplo de las elecciones en el congreso de EUA. Tenemos un modelo que usaremos para predecir la elección de \(1990\) basados en la de \(1988\).

Explicación del problema. EUA está dividido en \(435\) distritos congresionales, definimos la variable de interés \(y_i\) con \(i=1,...,n\), como la participación del partido Demócrata en el distrito \(i\) en \(1988\). La participación se calcula como el porcentaje de los votos correspondientes a los demócratas del total de votos que recibieron los demócratas y republicanos, esto es, se excluyen los votos a otros partidos.

El modelo del que simularemos se construyó usando datos de \(1986\) y \(1988\).

# Los datos están almacenados en 3 archivos correspondientes al año
paths <- dir("data/congress", full.names = TRUE)
paths <- set_names(paths, basename(paths))

# Leemos los datos y recodificamos variables
congress <- map_dfr(paths, read.table, quote = "\"", 
  stringsAsFactors = FALSE, .id = "year") %>%
  mutate(id = rep(1:435, 3),
         year = parse_number(year),          # año de la elección
         incumbency = ifelse(V3 == -9, NA, V3), # codificar NAs     
         dem_share = V4 / (V4 + V5)) %>%       # participación demócrata
  dplyr::select(id, year, incumbency, dem_share)

glimpse(congress)
#> Observations: 1,305
#> Variables: 4
#> $ id         <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ...
#> $ year       <dbl> 1986, 1986, 1986, 1986, 1986, 1986, 1986, 1986, 198...
#> $ incumbency <int> 1, 1, 1, -1, 1, -1, 0, -1, -1, 1, 1, 1, 1, 1, 1, 0,...
#> $ dem_share  <dbl> 0.745, 0.674, 0.696, 0.465, 0.391, 0.358, 0.549, 0....

# datos en forma horizontal
congress_share <- spread(dplyr::select(congress, -incumbency), year, dem_share)
colnames(congress_share) <- c("id", "share_86", "share_88", "share_90")
congress_inc <- spread(dplyr::select(congress, -dem_share), year, incumbency)
colnames(congress_inc) <- c("id", "inc_86", "inc_88", "inc_90")

# quitamos NAs
congress_h <- na.omit(left_join(congress_share, congress_inc))
#> Joining, by = "id"
glimpse(congress_h)
#> Observations: 431
#> Variables: 7
#> $ id       <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16...
#> $ share_86 <dbl> 0.745, 0.674, 0.696, 0.465, 0.391, 0.358, 0.549, 0.22...
#> $ share_88 <dbl> 0.772, 0.636, 0.665, 0.274, 0.264, 0.334, 0.632, 0.33...
#> $ share_90 <dbl> 0.714, 0.597, 0.521, 0.234, 0.477, 0.256, 0.602, 0.49...
#> $ inc_86   <int> 1, 1, 1, -1, 1, -1, 0, -1, -1, 1, 1, 1, 1, 1, 1, 0, 1...
#> $ inc_88   <int> 1, 1, 1, -1, -1, -1, 1, -1, -1, 1, 1, 1, 1, 1, 1, 1, ...
#> $ inc_90   <int> 1, 1, 0, -1, 0, -1, 0, -1, -1, 1, 1, 1, 1, 1, 1, 1, 1...

ggplot(congress_h, aes(x = share_86, y = share_88, color = factor(inc_86))) +
    geom_abline(color = "darkgray") +
    geom_point() +
    labs(color = "")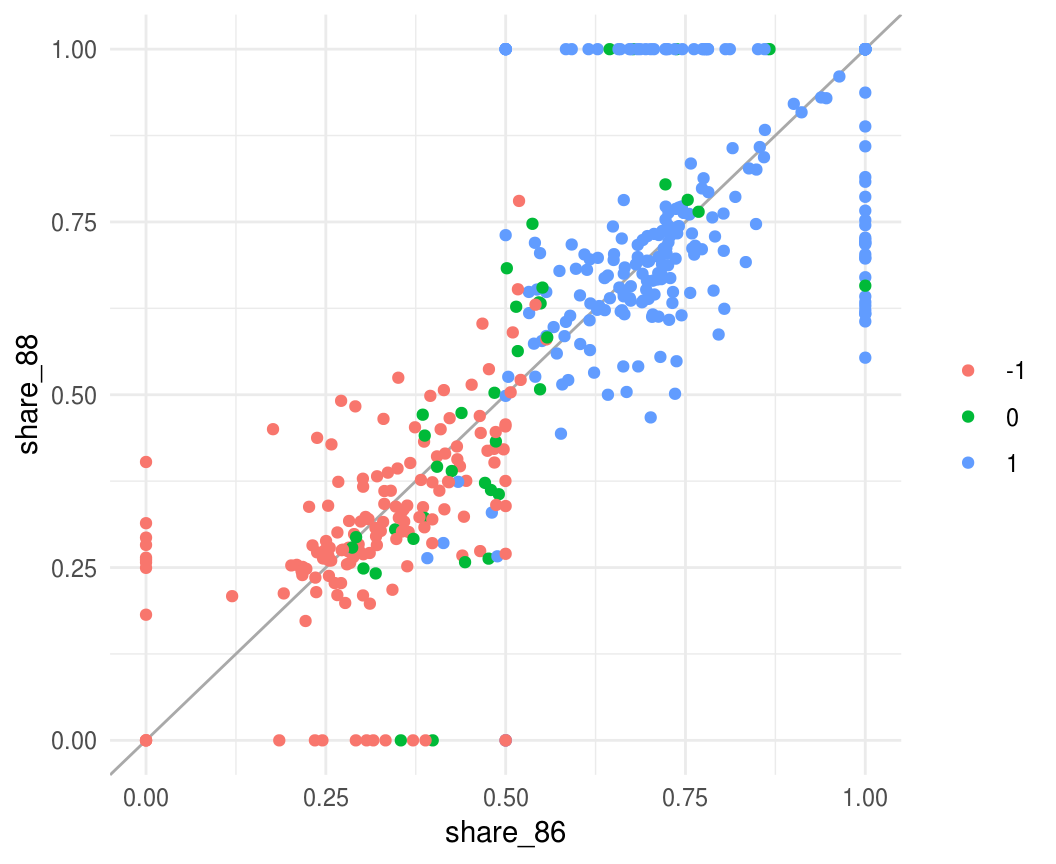

# quitamos las elecciones que no se compitieron
congress_h <- filter(congress_h, share_88 != 1 & share_88 != 0)

fit_88 <- lm(share_88 ~ share_86 + inc_88, data = congress_h)
summary(fit_88)
#> 
#> Call:
#> lm(formula = share_88 ~ share_86 + inc_88, data = congress_h)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -0.2416 -0.0428 -0.0059  0.0523  0.2263 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   0.3004     0.0151    19.9   <2e-16 ***
#> share_86      0.3858     0.0278    13.9   <2e-16 ***
#> inc_88        0.1043     0.0069    15.1   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.0774 on 351 degrees of freedom
#> Multiple R-squared:  0.846,  Adjusted R-squared:  0.845 
#> F-statistic:  965 on 2 and 351 DF,  p-value: <2e-16

Simulemos del modelo:

# Matriz X
X <- cbind(1, congress_h$share_88, congress_h$inc_90)
simula_modelo <- function(){
    sigma <- 0.08 * sqrt((351) / rchisq(1, 351))
    beta <- MASS::mvrnorm(1, mu = c(0.30, 0.39, 0.10), 
        Sigma = sigma ^ 2 * matrix(c(0.04, -0.07, 0.01, -0.07, 0.13, -0.02, 0.01, 
            -0.02, 0.01), nrow = 3))
    mu <- X %*% beta
    data_frame(id = 1:358, dem_share = rnorm(358, mu, sigma))
}

sims_congress <- rerun(2000, simula_modelo()) 
sims_congress <- sims_congress %>% bind_rows() %>% mutate(sim = rep(1:2000, each = 358))

ggplot(sims_congress, aes(x = reorder(id, dem_share), y = dem_share)) +
    geom_boxplot() +
    geom_hline(color = "red", yintercept = 0.5)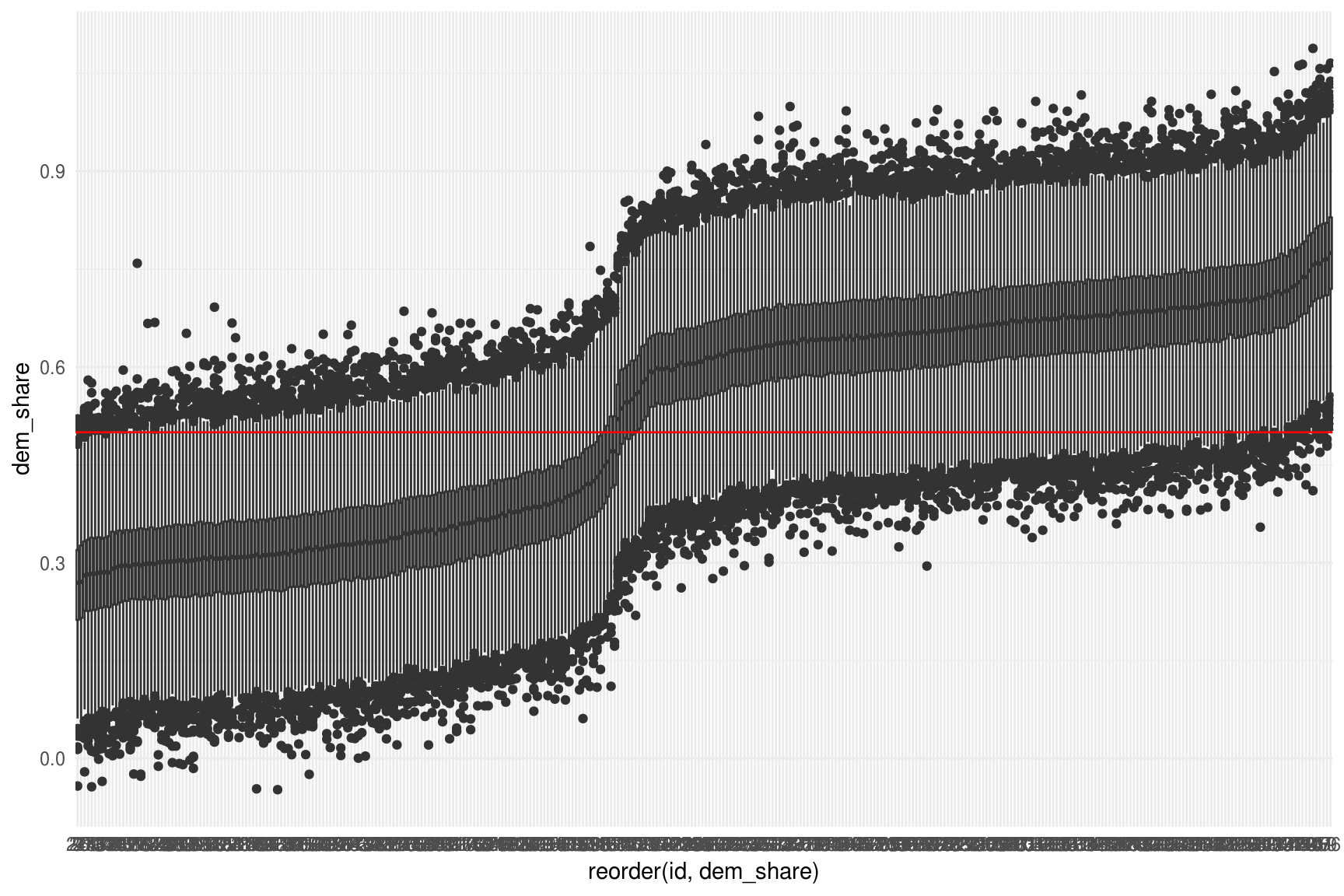

Podemos preguntarnos cuántas elecciones ganaron los demócratas en \(1990\): \(\sum I(\tilde{y} > 0.5)\)

sims_congress %>%
  group_by(sim) %>%
  mutate(wins = sum(dem_share > 0.5)) %>%
  ungroup() %>%
  summarise(mean_wins = mean(wins),
            median_wins = median(wins), 
            sd_wins = sd(wins))
#> # A tibble: 1 x 3
#>   mean_wins median_wins sd_wins
#>       <dbl>       <dbl>   <dbl>
#> 1      202.         202    3.78
sims_congress %>%
  group_by(sim) %>%
  mutate(wins = sum(dem_share > 0.5)) %>%
    pull(wins) %>% 
    qplot(binwidth = 1)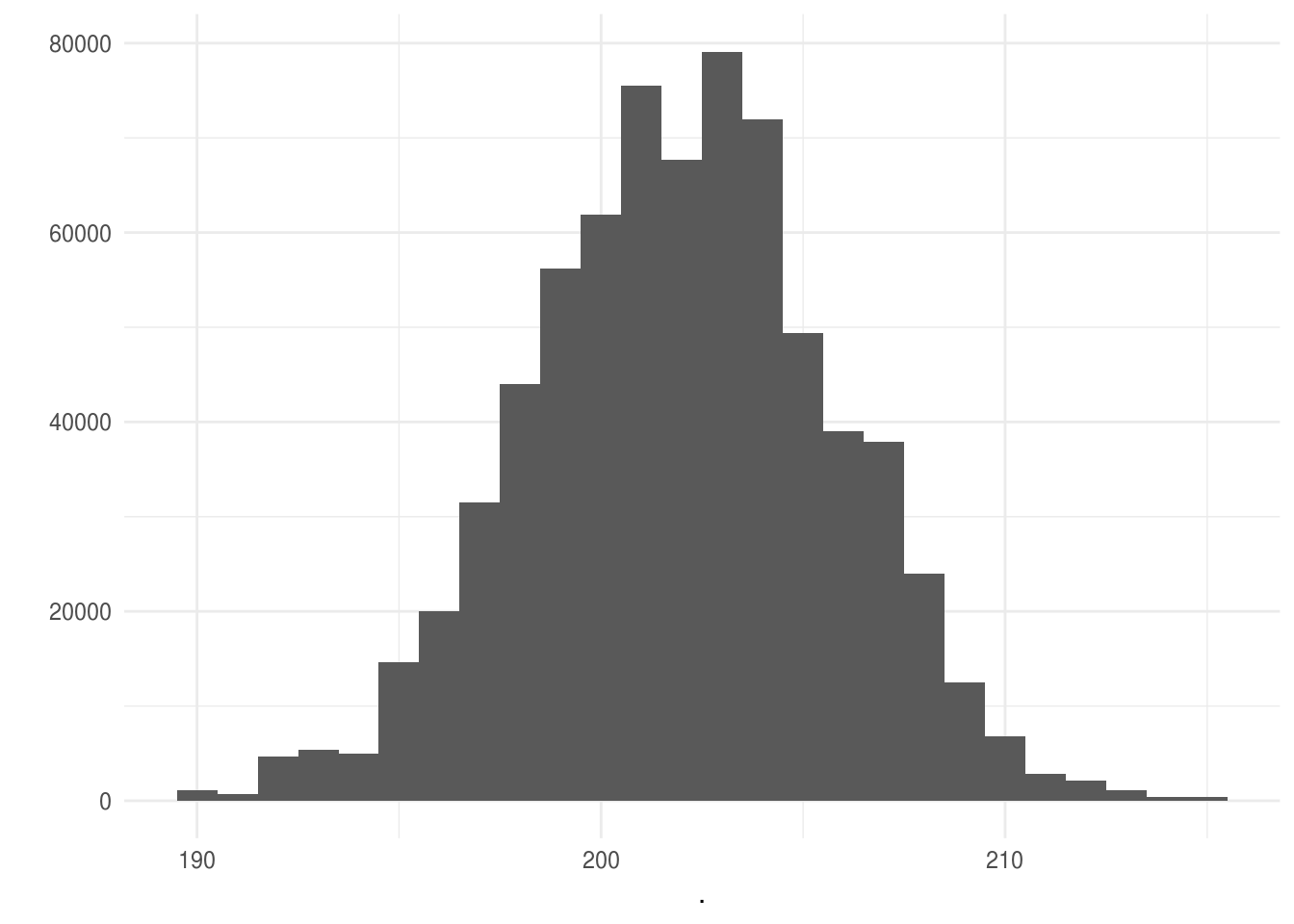

Veamos lo que ocurrió realmente

sum(congress_h$share_90 > 0.5)
#> [1] 207

La función sim() del paquete arm permite simular de modelos lineales y lineales generalizados.

sim_fit_88 <- arm::sim(fit_88, n.sims = 1000)
sim_fit_88@coef[1:10, ]
#>       (Intercept) share_86 inc_88
#>  [1,]       0.317    0.358 0.1078
#>  [2,]       0.300    0.377 0.1057
#>  [3,]       0.288    0.408 0.1109
#>  [4,]       0.302    0.379 0.1078
#>  [5,]       0.302    0.377 0.1086
#>  [6,]       0.297    0.388 0.1042
#>  [7,]       0.283    0.423 0.0978
#>  [8,]       0.307    0.368 0.1095
#>  [9,]       0.305    0.372 0.1077
#> [10,]       0.283    0.430 0.0933
sim_fit_88@sigma[1:10]
#>  [1] 0.0812 0.0799 0.0747 0.0751 0.0807 0.0815 0.0760 0.0766 0.0804 0.0790

Referencias

Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Vol. Analytical methods for social research. New York: Cambridge University Press.