10.4 Aproximación por cuadrícula

Supongamos que la distribución beta no describe nuestras creencias de manera adecuada. Por ejemplo, mis creencias podrían estar mejor representadas por una distribución trimodal: la moneda esta fuertemente sesgada hacia sol, fuertemente sesgada hacia águila o es justa. No hay parámetros en una beta que puedan describir este patrón.

Exploraremos entonces una técnica de aproximación numérica de la distribución posterior que consiste en definir la distribución inicial en una cuadrícula de valores de \(\theta\). En este método no necesitamos describir nuestras creencias mediante una función matemática ni realizar integración analítica. Suponemos que existe únicamente un número finito de valores de \(\theta\) que creemos que pueden ocurrir (el primer ejemplo que estudiamos usamos esta técnica). Es así que la regla de Bayes se escribe como:

\[p(x|\theta)=\frac{p(x|\theta)p(\theta)}{\sum_{\theta}p(x|\theta)p(\theta)}\]

Entonces, si podemos discretizar una distribución inicial continua mediante una cuadrícula de masas de probabilidad discreta podemos usar la versión discreta de la regla de Bayes. El proceso consiste en dividir el dominio en regiones, crear un rectángulo con la altura correspondiente al valor de la densidad en el punto medio. Aproximamos el área de cada región mediante la altura del rectángulo.

# N = 14, z = 11, a = 1, b = 1
N = 14; z = 11
inicial <- data.frame(theta = seq(0.05, 1, 0.05), inicial = rep(1/20, 20))
dists_h <- inicial %>%
    mutate(
        verosimilitud = theta ^ z * (1 - theta) ^ (N - z), # verosimilitud 
        posterior = (verosimilitud * inicial) / sum(verosimilitud * inicial)
        )  
dists <- dists_h %>% # base de datos larga
    gather(dist, valor, inicial, verosimilitud, posterior) %>% 
    mutate(dist = factor(dist, levels = c("inicial", "verosimilitud", "posterior")))

ggplot(dists, aes(x = theta, y = valor)) +
    geom_point() +
    facet_wrap(~ dist, scales = "free") +
    scale_x_continuous(expression(theta), breaks = seq(0, 1, 0.2)) +
    labs(y = "")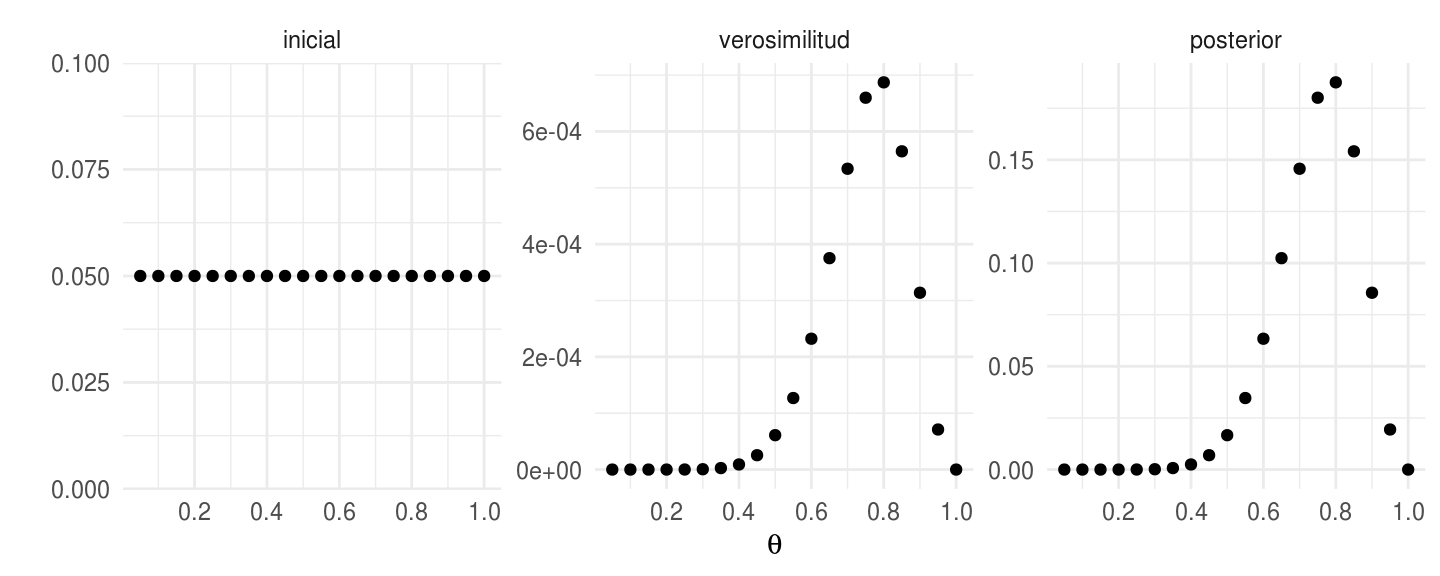

y lo podemos comparar con la versión continua (distribución beta).

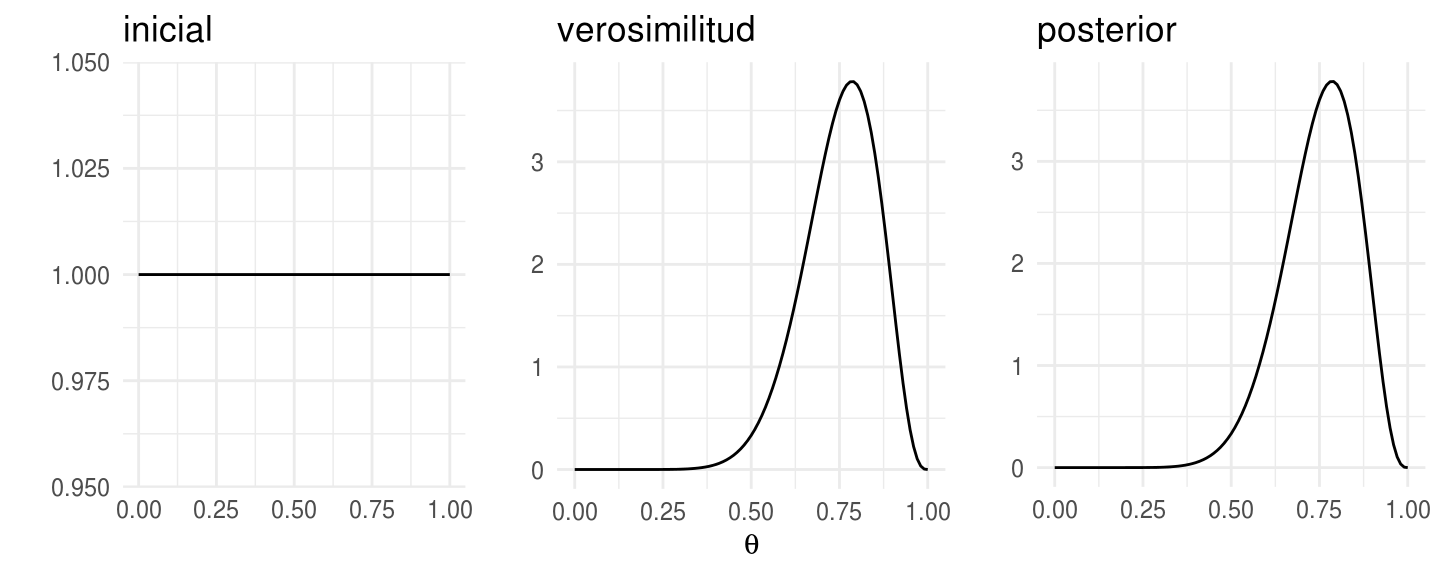
En cuanto a la estimación, la tabla de probabilidades nos da una estimación para los valores de los parámetros. Podemos calcular la media de \(\theta\) como el promedio ponderado por las probabilidades:

\(\bar{\theta}=\sum_{\theta} \theta p(\theta|x)\)

head(dists_h)
#>   theta inicial verosimilitud posterior
#> 1  0.05    0.05      4.19e-15  1.14e-12
#> 2  0.10    0.05      7.29e-12  1.99e-09
#> 3  0.15    0.05      5.31e-10  1.45e-07
#> 4  0.20    0.05      1.05e-08  2.86e-06
#> 5  0.25    0.05      1.01e-07  2.75e-05
#> 6  0.30    0.05      6.08e-07  1.66e-04
sum(dists_h$posterior * dists_h$theta)
#> [1] 0.75

Ahora para intervalos de probabilidad, debido a que estamos usando masas discretas, la suma de las masas en un intervalo usualmente no será igual a \(95\%\) y por tanto elegimos los puntos tales que la masa sea mayor a igual a \(95\%\) y la masa total sea lo menor posible, en nuestro ejemplo podemos usar cuantiles.

dist_cum <- cumsum(dists_h$posterior) #vector de distribución acumulada
lb <- which.min(dist_cum < 0.05) - 1
ub <- which.min(dist_cum < 0.975)
dists_h$theta[lb]
#> [1] 0.5
dists_h$theta[ub]
#> [1] 0.9

Para el problema de predicción, la probabilidad predictiva para el siguiente valor \(y\) es simplemente la probabilidad de que ocurra dicho valor ponderado por la probabilidad posterior correspondiente:

\[p(y|x)=\int p(y|\theta)p(\theta|x)d\theta\] \[\approx \sum_{\theta} p(y|\theta)p(\theta|x)\]

Calcula la probabilidad predictiva para \(y=1\) usando los datos del ejemplo.

Finalmente, para la comparación de modelos la integral que define la evidencia

\[p(x|M)=\int p(x|\theta,M)p(\theta|M)d\theta\]

se convierte en una suma

\[p(x|M)\approx \sum_{\theta} p(x|\theta,M)p(\theta|M)d\theta\]

# calcula el factor de Bayes para el experimento Bernoulli Modelos M1 y M2
factorBayes <- function(M, s){
  evidencia <- rbind(p_M1, p_M2) %>% # base de datos horizontal
    group_by(modelo) %>%
    mutate(
      Like = theta ^ s * (1 - theta) ^ (M - s), # verosimilitud 
      posterior = (Like * prior) / sum(Like * prior)
    ) %>%
    summarise(evidencia = sum(prior * Like))
  print(evidencia)
  return(evidencia[1, 2] / evidencia[2, 2])
}

factorBayes(50, 25)
#> # A tibble: 2 x 2
#>   modelo evidencia
#>   <chr>      <dbl>
#> 1 M1      4.44e-16
#> 2 M2      2.75e-16
#>   evidencia
#> 1      1.61