5.3 Simulación para el cálculo de probabilidades

En el ejemplo anterior vimos que puede ser sencillo usar simulación para calcular probabilidades, pues usando la interpretación de frecuencia relativa simplemente hace falta simular el experimento y contar los casos favorables entre el total de casos.

Simulación para el cálculo de probabilidades:

  1. Definir el espacio de resultados.

  2. Describir el mecanismo que genera los resultados, esto incluye entender los pasos que involucran azar y los que no.

  3. Replicar el experimento con código, siguiendo el conocimiento elicitado en 1 y 2.

  4. Repetir el paso 3 \(n\) veces y calcular la frecuencia relativa de éxitos, estimando así la probabilidad.

Para el paso 2, en R suelen ser de utilidad las funciones runif y sample(), revisa la ayuda de estas funciones.

Ejemplo: comité

Un comité de 5 personas será seleccionado de un grupo de 6 hombres y 9 mujeres. Si la selección es aleatoria, ¿cuál es la probabilidad de que el comité este conformado por 3 hombres y 2 mujeres?

  1. El espacio de resultados es \(\Omega = \{M_1M_2M_3M_4M_5, M_2M_3M_4M_5M_6,... H_1,H_2H_3H_4H_5,H_2H_3H_4H_5H_6\}\).

  2. Se seleccionan 5 integrantes al azar del conjunto de hombres y mujeres, es claro que cada persona solo puee estar una vez.

candidatos <- c(paste("M", 1:9, sep = "_"), paste("H", 1:6, sep = "_"))
sample(candidatos, 5, replace = FALSE)
#> [1] "H_1" "M_7" "H_5" "M_4" "M_3"
comite <- function(){
    candidatos <- c(paste("M", 1:9, sep = "_"), paste("H", 1:6, sep = "_"))
    comite <- sample(candidatos, 5, replace = FALSE)
    n_mujeres <- sum(substr(comite, 1, 1) == "M")
    n_mujeres == 2
}

rerun(1000, comite()) %>% flatten_dbl() %>% mean()
#> [1] 0.219

Ejemplo: La ruina del jugador

  • Un jugador tiene $100, y va a apostar en un juego donde la probabilidad de ganar es p = 0.47 (e.g. una ruleta 18/38), si gana recibe el doble de lo que arriesgó, si no gana pierde todo lo que apostó.

  • Cada vez que juega puede apostar cualquier cantidad siempre y cuando aún cuente con dinero.

  • El jugador dejará de jugar cuando su capital sea $0 o cuando gane $200.

  • El jugador busca una estrategia que le ayude a aumentar su probabilidad de ganar y te pregunta: ¿Cuál es la probabilidad de ganar si apuesto en incrementos de $5 cada vez que apuesto?

Siguiendo los pasos enunciados:

  1. El espacio de resultados es \(\Omega = \{GGGGGGGGGGGGGGGGGGGG, PGGGGGGGGGGGGGGGGGGGGGG, GPGGGGGGGGGGGGGGGGGGGGG, ...\}\).

  2. El jugador juega mientras tenga capital y este sea menor a $200, el monto de la apuesta está fijo en $5, no importa el capital en cada momento. La componente aleatoria involucra si gana cada uno de los juegos y esto ocurre con probabilidad 0.47.

apostar <- function(dinero = 100, apuesta = 5, tope = 200){
    while(0 < dinero & dinero < tope){
        if(sample(1:38, 1) <= 18){
            dinero <- dinero + apuesta
        } 
        else{
            dinero <- dinero - apuesta
        }
    }
    dinero > 0
}
n_juegos <- 5000
juegos <- rerun(n_juegos, apostar()) %>% flatten_dbl()
mean(juegos)
#> [1] 0.114

# incrementos de 50?
juegos <- rerun(n_juegos, apostar(apuesta = 50)) %>% flatten_dbl()
mean(juegos)
#> [1] 0.443

La solución analítica la pueden leer en este documento de caminatas aleatorias:

p = 0.47
1 - (1 - (p / (1 - p)) ^ (100 / 5)) / (1 - (p / (1 - p)) ^ (200 / 5)) # apostando de 5 en 5
#> [1] 0.083
1 - (1 - (p / (1 - p)) ^ (100 / 50)) / (1 - (p / (1 - p)) ^ (200 / 50)) # apostando de 50 en 50
#> [1] 0.44

Cumpleaños. ¿Cuántas personas debe haber en un salón para que la probabilidad de encontrar 2 con el mismo cumpleaños sea 0.5? Supuestos:

  • Mismo cumpleaños implica mismo día y mes.

  • No hay años bisiestos.

  • La probabilidad de que alguien nazca un día dado es la misma para todos los días del año.

Chabelo (Monty Hall) Supongamos que estamos jugando las catafixias de Chabelo, en este juego hay 3 catafixias: 2 de ellas están vacías y una tiene un premio:

  1. El juego comienza cuando escoges una catafixia.
  2. A continuación Chabelo abre una catafixia vacía de las dos catafixias restantes.

  3. Tu eliges si te mantienes con tu catafixia o cambias a la otra que continúa cerrada. Chabelo abre tu segunda elección de catafixia y se revela si ganaste.

    ¿Cuál es la probabilidad de que ganes si cambias de catafixia?

Urna: 10 personas (con nombres distintos) escriben sus nombres y los ponen en una urna, después seleccionan un nombre (al azar).

  • Sea A el evento en el que ninguna persona selecciona su nombre, ¿Cuál es la probabilidad del evento A?

  • Supongamos que hay 3 personas con el mismo nombre, ¿Cómo calcularías la probabilidad del evento A en este nuevo experimento?

  • El señor J. tiene 2 cachorros, el mayor es hembra. ¿Cuál es la probabilidad de que los dos sean hembra?

  • La señora K. tiene 2 cachorros, al menos uno es macho. ¿Cuál es la probabilidad de que los dos sean macho?

Podemos generalizar las definiciones de equiprobable al caso continuo, como ejemplo supongamos que se lanza un dado a un table cuadrandgular de lado 2, ¿cuál es la probabilidad de que el dado caiga en el círculo de radio 1 inscrito en un cuadrado de lado 2?

tablero <- ggplot() + 
    ggforce::geom_circle(aes(x0 = 0, y0 = 0, r = 1)) +
    geom_rect(aes(xmin = -1, xmax = 1,   ymin = -1, ymax = 1),   fill = "white", 
        color = "black", alpha = 0.5) +
    coord_equal()
ggsave("imagenes/tablero.png", tablero, width = 3, height = 3)
knitr::include_graphics("imagenes/tablero.png")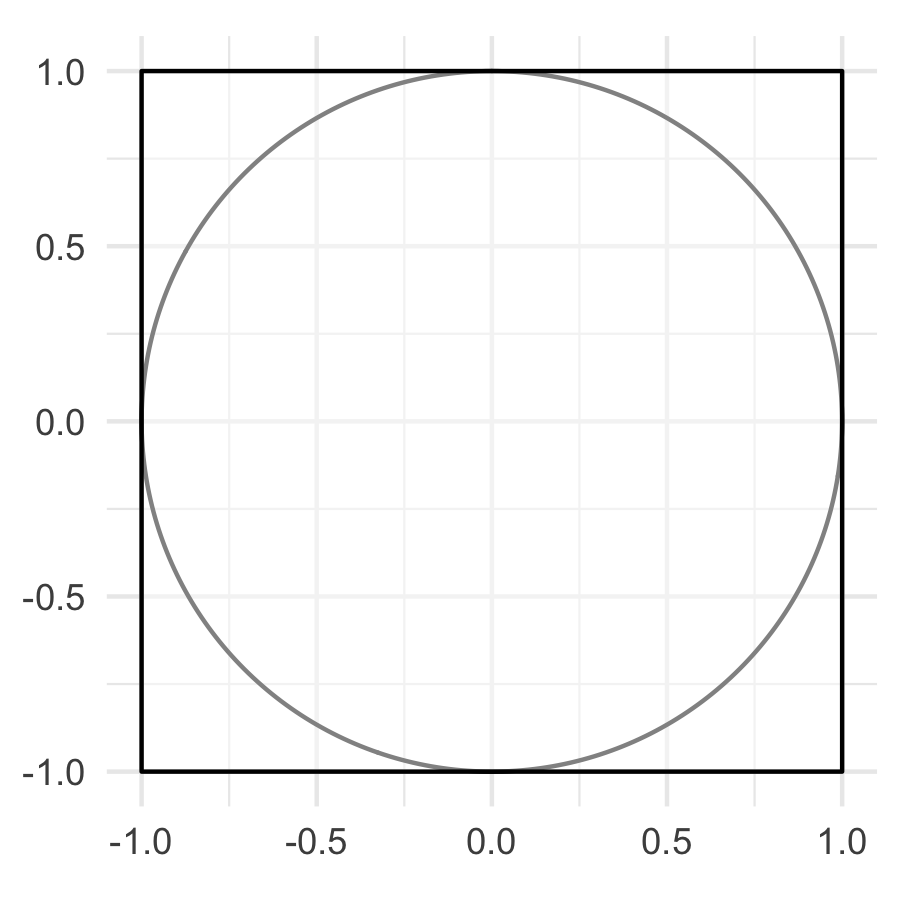

En este caso usamos áreas relativas para calcular la probabilidad: denotemos C al evento tal que el dardo cae en el círculo, entonces:

\[P(B) = \frac{Área(B)}{Área(\Omega)}\] ¿Y simulando?

circunferencia <- function(){
  x <- runif(1) * sample(c(-1, 1), 1)
  y <- runif(1) * sample(c(-1, 1), 1)
  sqrt(x ^ 2 + y ^ 2) < 1
}
rerun(10000, circunferencia()) %>% flatten_dbl() %>% mean()
#> [1] 0.784
dardos <- data_frame(x = runif(1000, -1, 1), y = runif(1000, -1, 1), 
    en_circulo = sqrt(x ^ 2 + y ^ 2) < 1)

tablero_dardos <- tablero +
    geom_point(data = dardos, aes(x, y, color = en_circulo), alpha = 0.5, 
        show.legend = FALSE)

ggsave("imagenes/tablero_dardos.png", tablero_dardos, width = 3, height = 3)
knitr::include_graphics("imagenes/tablero_dardos.png")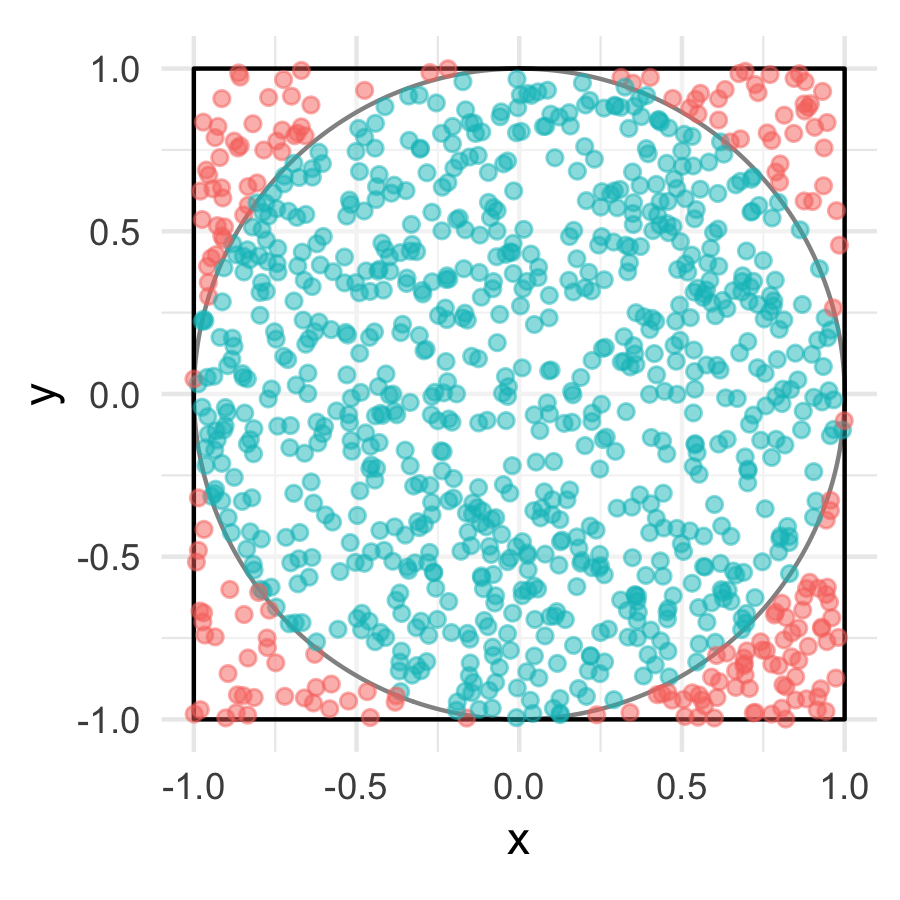

Ahora, en el ejemplo de los dardos es más realista pensar que la probabilidad de que el dardo caiga en un segmento de la zona central no es la misma a que caiga en un segmento de igual área en las orillas.

tablero_zonas <- tablero +
    geom_rect(aes(xmin = -1, xmax = -0.8,   ymin = -1, ymax = -0.8), 
        fill = "red", alpha = 0.5) + 
    geom_rect(aes(xmin = -.1, xmax = 0.1,   ymin = -0.1, ymax = 0.1), 
        fill = "red", alpha = 0.5)
ggsave("imagenes/tablero_zonas.png", tablero_zonas, width = 3, height = 3)
knitr::include_graphics("imagenes/tablero_zonas.png")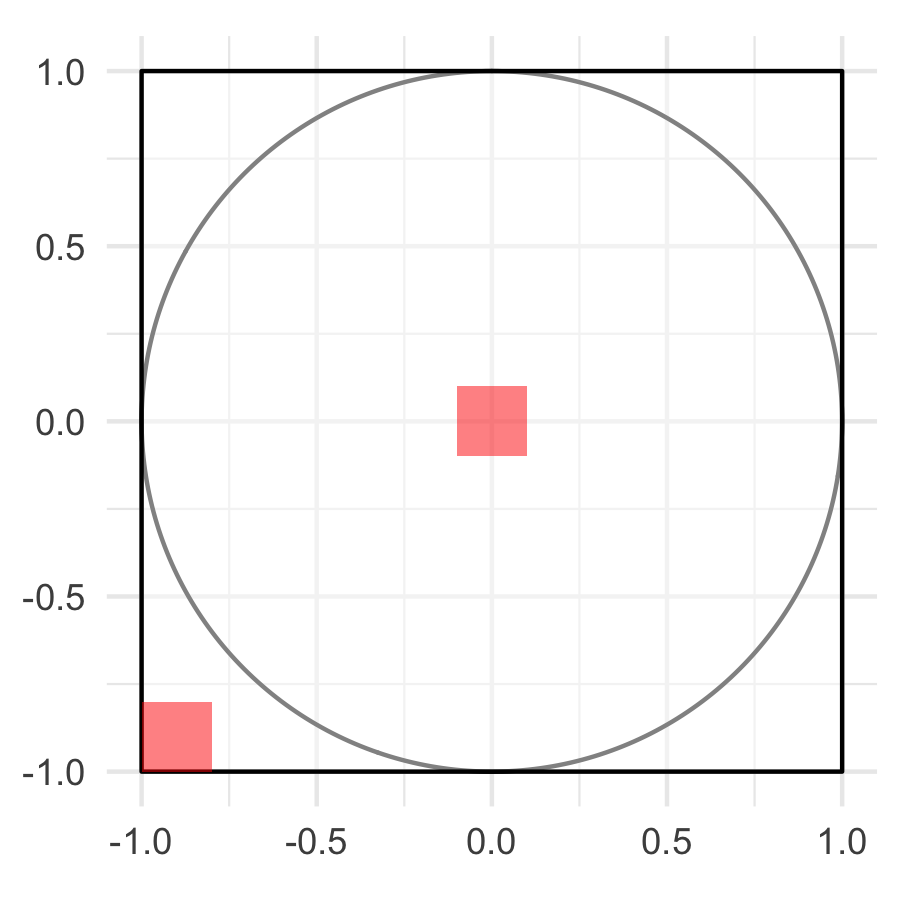

La definición de probabilidad como área relativa no se puede usar en estos casos, sin embargo, el enfoque de simulación se continúa manteniendo.

Comencemos con el caso del dardo univariado.

unif <- ggplot() +
    geom_rect(aes(xmin = 0.3, xmax = 0.6,   ymin = 0, ymax = 1), 
        fill = "red", alpha = 0.5) +
    xlim(0, 1)
unif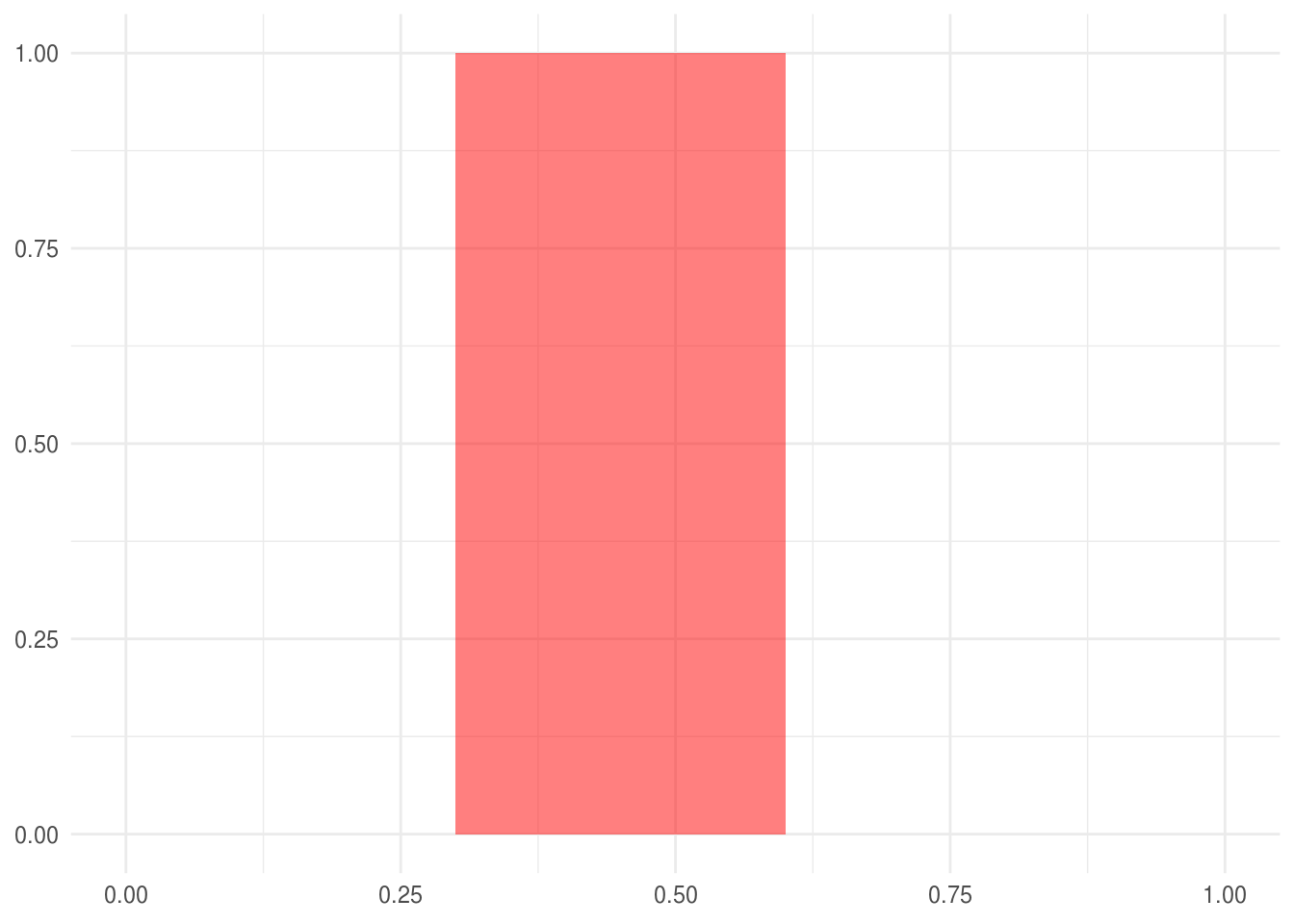

En este caso de área relativa, calculamos la probabilidad cómo el área sombreada

\[P([a, b]) = \frac{b-a}{1} = \int_a^b 1dx\]

Ahora, si el dardo cae en ciertas zonas con mayor probabilidad:

ggplot(data_frame(x = c(0 , 1)), aes(x)) + 
    stat_function(fun = dbeta, args = list(shape1 = 5, shape2 = 2)) +
    geom_rect(data = NULL, aes(xmin = 0, xmax = 1, ymin = 0, ymax = 1), 
        fill = "red", alpha = 0.2)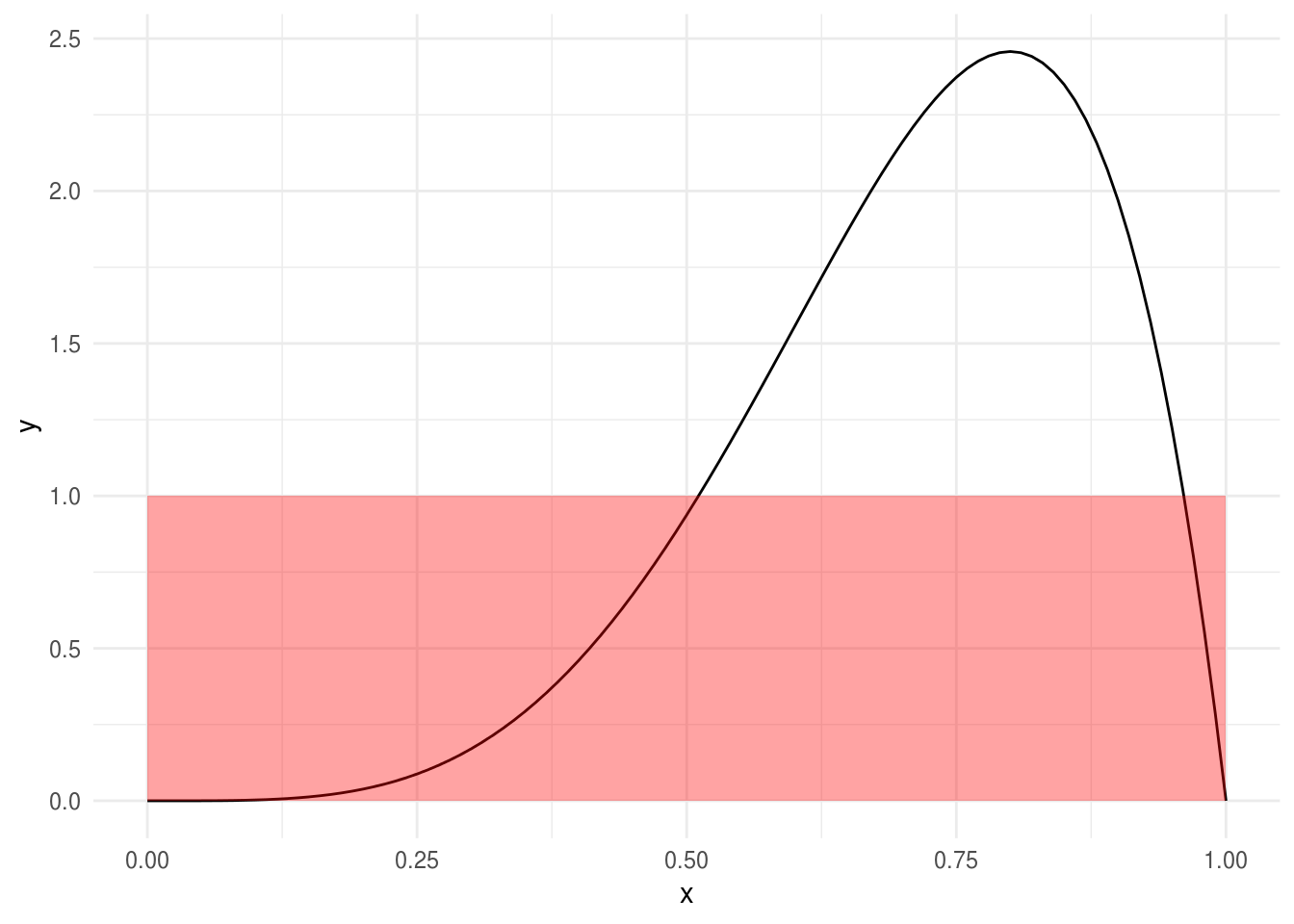

\[P([a,b])=\int_a^bf(x)dx\] Y lo podemos calcular con simulación, por ejemplo la probabilidad de x en [0.2, 0.5]:

curva <- function(){
    x <- runif(1)
    y <- runif(1) * 2.5
    while(dbeta(x, 5, 2) < y){
        x <- runif(1)
        y <- runif(1) * 2.5
    }
    x
}

sims_x <- rerun(5000, curva()) %>% flatten_dbl()
mean(sims_x > 0.2 & sims_x < 0.5)
#> [1] 0.104
data_frame(x = runif(1000), y = runif(1000) * 2.5, dentro = dbeta(x, 5, 2) > y, 
    en_int = dentro * (x > 0.2 & x < 0.5), cat = case_when(!dentro ~ "a", 
        dentro & en_int ~ "b", TRUE ~ "c")) %>% 
    ggplot()+ 
    stat_function(fun = dbeta, args = list(shape1 = 5, shape2 = 2)) +
        geom_point(aes(x, y, color = cat), alpha = 0.5, 
            show.legend = FALSE)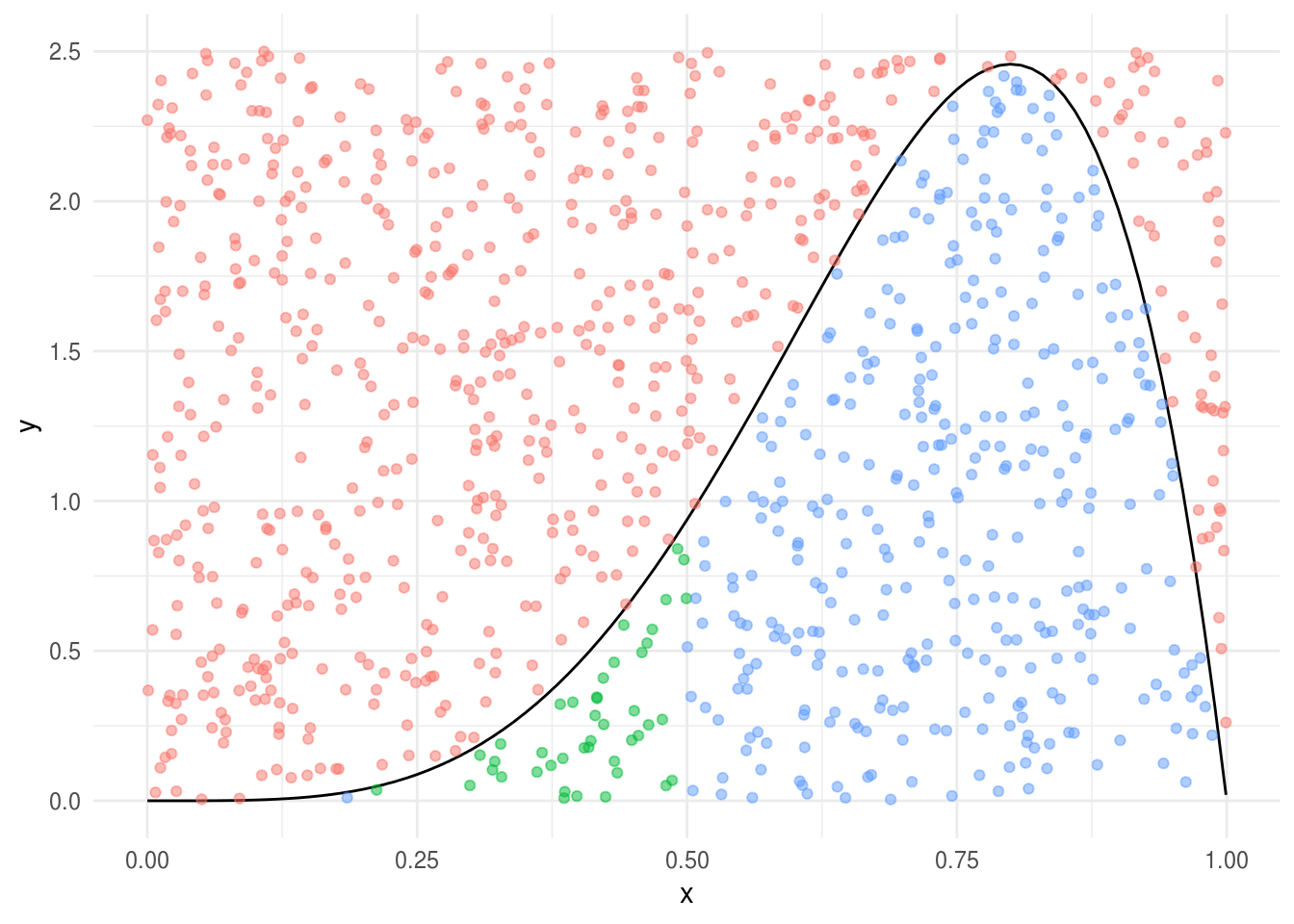

En el caso discreto: Supongamos que el proceso de selección del comité tiene sesgo, las mujeres se seleccionan con mayor probabilidad que los hombres:

comite <- function(){
    candidatos <- c(paste("M", 1:9, sep = "_"), paste("H", 1:6, sep = "_"))
    comite <- sample(candidatos, 5, replace = FALSE, 
        prob = c(rep(2, 9), rep(1, 6)))
    n_mujeres <- sum(substr(comite, 1, 1) == "M")
    n_mujeres == 2
}

rerun(1000, comite()) %>% flatten_dbl() %>% mean()
#> [1] 0.094