14-Ejercicios clase modelos jerárquicos
Implementaremos varios modelos en JAGS o Stan, la base de datos que usaremos contiene información de mediciones de radón (activity) y del suelo en el que se hicieron las mediciones (floor = \(0\) casas con sótano, floor = \(1\) casas sin sótano), las mediciones corresponden a \(919\) hogares muestreados de \(85\) condados de Minnesota, (este es ejercicio se tomó de Gelman and Hill (2007)). El objetivo es construir un modelo de regresión en el que la medición de radón es la variable independiente y el tipo de suelo es la covariable.
- Iniciaremos con un modelo de regresión de unidades iguales, este modelo ignora la variación en los niveles de radón entre los condados.
\[y_i \sim N(\alpha + \beta x_i, \sigma_y^2) \]
# preparación de los datos
library(R2jags)
#> Loading required package: rjags
#> Loading required package: coda
#> Linked to JAGS 4.3.0
#> Loaded modules: basemod,bugs
#>
#> Attaching package: 'R2jags'
#> The following object is masked from 'package:coda':
#>
#> traceplot
radon <- read.csv("data/radon.csv")
# creamos variable de condado como entrero consecutivo para iterar
radon$county <- as.numeric(factor(radon$cntyfips))
y <- log(ifelse (radon$activity == 0, 0.1, radon$activity))
n <- nrow(radon)
x <- radon$floor
J <- length(unique(radon$county))
county <- radon$countymodelo_1 <-
'
model{
for(i in 1 : n) {
y[i] ~ dnorm(y.hat[i], tau.y)
y.hat[i] <- a + b * x[i]
}
a ~ dnorm(0, 0.0001)
b ~ dnorm(0, 0.0001)
tau.y <- pow(sigma.y, -2)
sigma.y ~ dunif(0, 100)
}
'
cat(modelo_1, file = 'modelo_1.bugs')# llamar a jags
radon_1_data <- list(n = n, y = y, x = x)
radon_1_inits <- function(){
list(a = rnorm(1), b = rnorm(1), sigma.y = runif(1))}
radon_1_parameters <- c("a", "b", "sigma.y")
radon_1_jags <- jags(data = radon_1_data, inits= radon_1_inits,
parameters.to.save = radon_1_parameters, model.file = "modelo_1.bugs",
n.iter = 1000)
#> module glm loaded
#> Compiling model graph
#> Resolving undeclared variables
#> Allocating nodes
#> Graph information:
#> Observed stochastic nodes: 919
#> Unobserved stochastic nodes: 3
#> Total graph size: 1852
#>
#> Initializing model
radon_1_jags
#> Inference for Bugs model at "modelo_1.bugs", fit using jags,
#> 3 chains, each with 1000 iterations (first 500 discarded)
#> n.sims = 1500 iterations saved
#> mu.vect sd.vect 2.5% 25% 50% 75% 97.5%
#> a 1.327 0.030 1.268 1.307 1.327 1.347 1.387
#> b -0.611 0.075 -0.758 -0.662 -0.610 -0.558 -0.466
#> sigma.y 0.824 0.020 0.786 0.811 0.824 0.837 0.864
#> deviance 2250.220 2.606 2247.252 2248.296 2249.672 2251.319 2256.846
#> Rhat n.eff
#> a 1 1500
#> b 1 1500
#> sigma.y 1 1500
#> deviance 1 1400
#>
#> For each parameter, n.eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
#>
#> DIC info (using the rule, pD = var(deviance)/2)
#> pD = 3.4 and DIC = 2253.6
#> DIC is an estimate of expected predictive error (lower deviance is better).- Después pasamos a un modelo de unidades independientes, en este simplemente incluímos indicadoras a nivel condado.
\[y_i \sim N(\alpha_{j[i]} + \beta x_i, \sigma_y^2)\]
modelo_2 <-
'
model{
for(i in 1 : n) {
y[i] ~ dnorm(y.hat[i], tau.y)
y.hat[i] <- a[county[i]] + b * x[i]
}
b ~ dnorm(0, 0.001)
tau.y <- pow(sigma.y, -2)
sigma.y ~ dunif(0, 100)
for(j in 1:J){
a[j] ~ dnorm(0, 0.001)
}
}
'
cat(modelo_2, file = 'modelo_2.bugs')radon_2_data <- list(n = n, J = J, y = y, county = county, x = x)
radon_2_inits <- function(){
list(a = rnorm(J), b = rnorm(1), sigma.y = runif(1))}
radon_2_parameters <- c("a", "b", "sigma.y")
radon_2_jags <- jags(data = radon_2_data, inits= radon_2_inits,
parameters.to.save = radon_2_parameters, model.file = "modelo_2.bugs",
n.iter = 1000)
#> Compiling model graph
#> Resolving undeclared variables
#> Allocating nodes
#> Graph information:
#> Observed stochastic nodes: 919
#> Unobserved stochastic nodes: 87
#> Total graph size: 2999
#>
#> Initializing model
plot(radon_2_jags)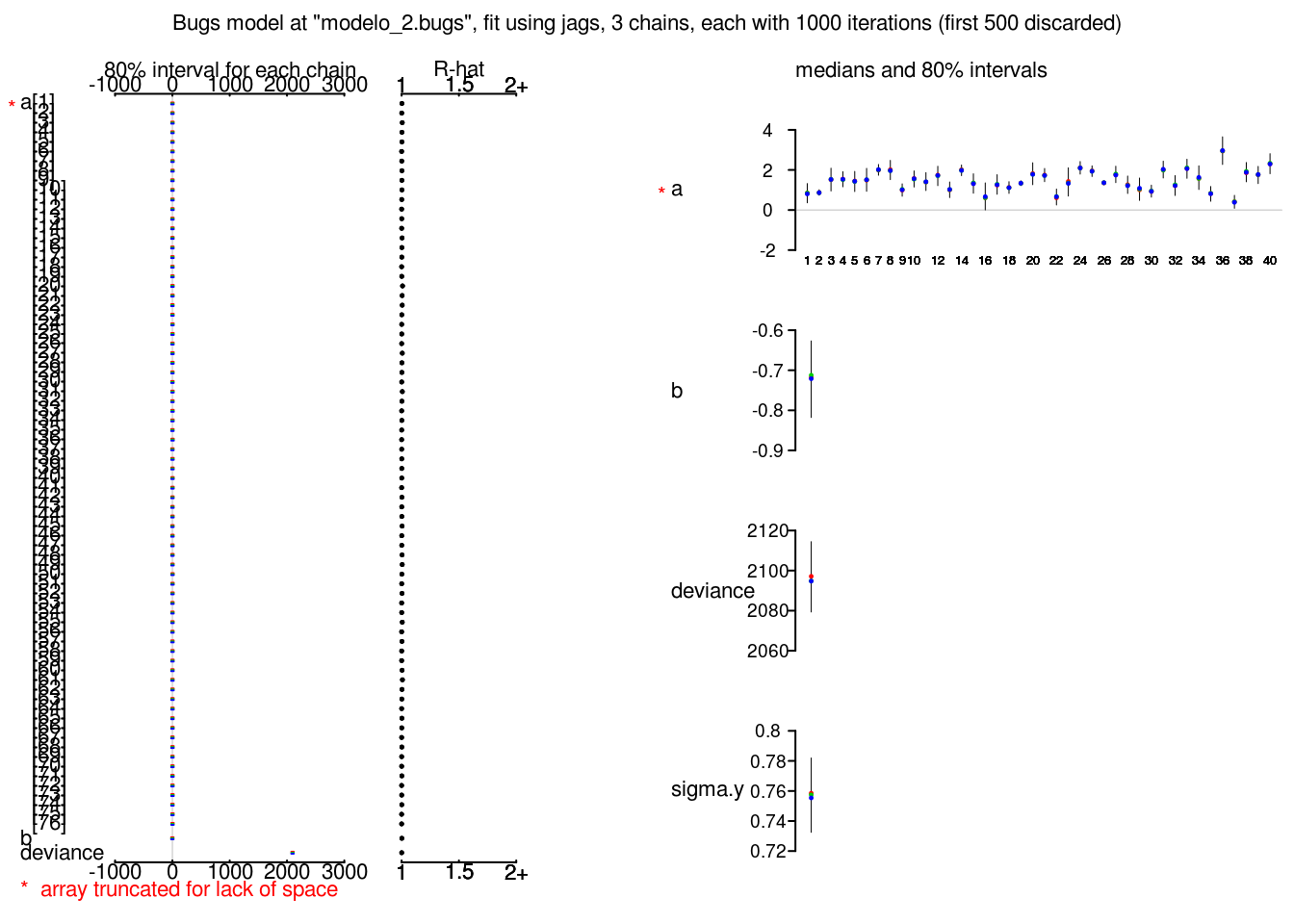
- Añadimos una estructura jerárquica al modelo: \[y_i \sim N(\alpha_{j[i]} + \beta x_i, \sigma_y^2) \] \[\alpha_j \sim N(\mu_{\alpha}, \sigma_{\alpha}^2)\]
modelo_3 <-
'
model{
for(i in 1 : n) {
y[i] ~ dnorm(y.hat[i], tau.y)
y.hat[i] <- a[county[i]] + b * x[i]
}
b ~ dnorm(0, 0.0001)
tau.y <- pow(sigma.y, -2)
sigma.y ~ dunif(0, 100)
for(j in 1:J){
a[j] ~ dnorm(mu.a, tau.a)
}
mu.a ~ dnorm(0, 0.0001)
tau.a <- pow(sigma.a, -2)
sigma.a ~ dunif(0, 100)
}
'
cat(modelo_3, file = 'modelo_3.bugs')radon_inits <- function(){
list(a = rnorm(J), b = rnorm(1), mu.a = rnorm(1), sigma.y = runif(1),
sigma.a = runif(1))}
radon_parameters <- c("a", "b", "mu.a", "sigma.y", "sigma.a")
radon_3_jags <- jags(data = radon_2_data, inits= radon_inits,
parameters.to.save = radon_parameters, model.file = "modelo_3.bugs",
n.iter = 1000, n.chains = 2)
#> Compiling model graph
#> Resolving undeclared variables
#> Allocating nodes
#> Graph information:
#> Observed stochastic nodes: 919
#> Unobserved stochastic nodes: 89
#> Total graph size: 3002
#>
#> Initializing model
plot(radon_3_jags)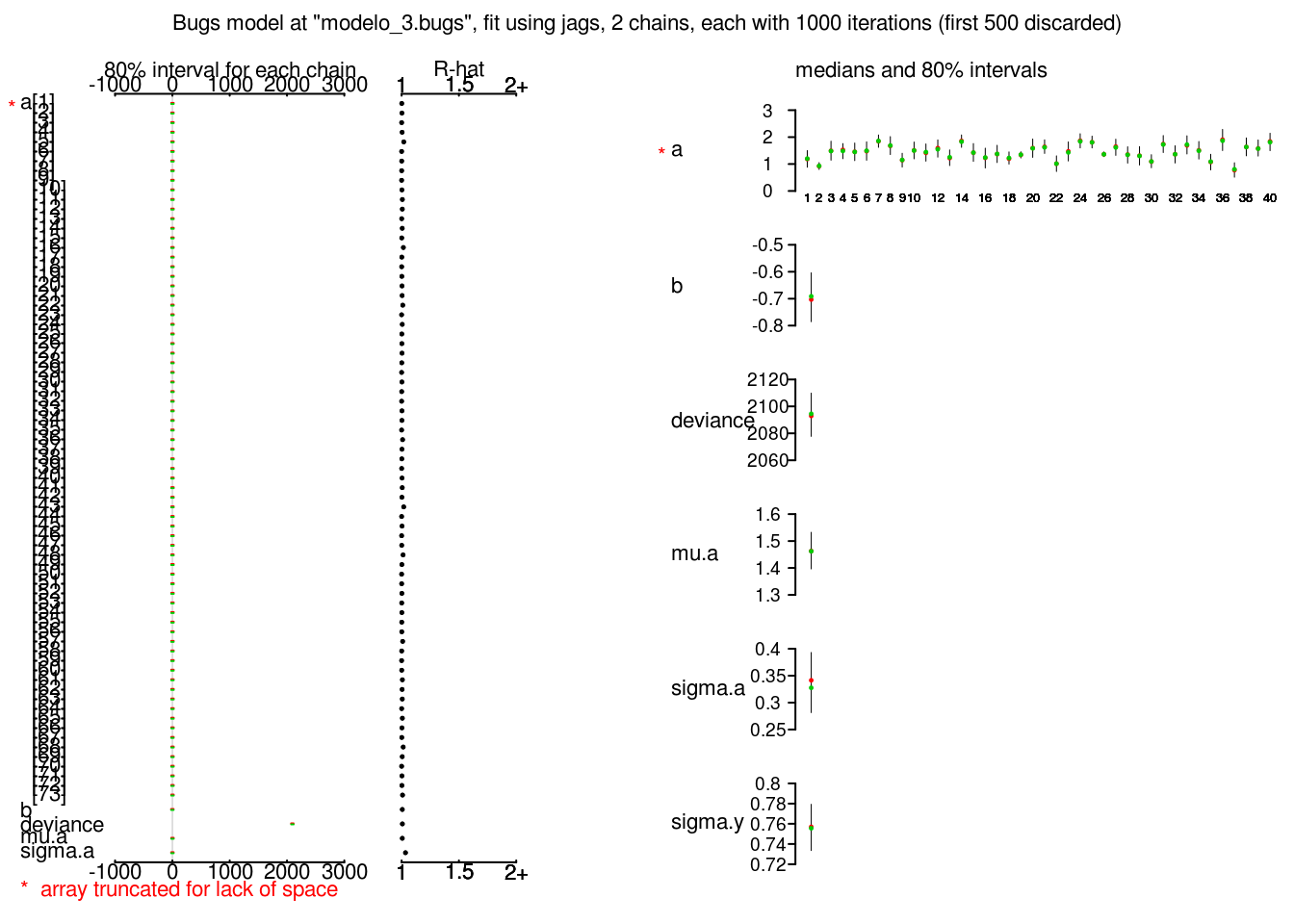
- Incorporamos una covariable \(u_j\) a nivel grupo, en este caso elegiremos una medición de uranio a nivel condado (Uppm).
\[y_i \sim N(\alpha_{j[i]} + \beta x_i, \sigma_y^2) \] \[\alpha_j \sim N(\gamma_0 + \gamma_{1}u_j, \sigma_{\alpha}^2)\]
modelo_4 <-
'
model{
for(i in 1 : n) {
y[i] ~ dnorm(y.hat[i], tau.y)
y.hat[i] <- a[county[i]] + b * x[i]
}
b ~ dnorm(0, 0.0001)
tau.y <- pow(sigma.y, -2)
sigma.y ~ dunif(0, 100)
for(j in 1:J){
a[j] ~ dnorm(a.hat[j], tau.a)
a.hat[j] <- g.0 + g.1 * u[j]
}
g.0 ~ dnorm(0, 0.0001)
g.1 ~ dnorm(0, 0.0001)
tau.a <- pow(sigma.a, -2)
sigma.a ~ dunif(0, 100)
}
'
cat(modelo_4, file = 'modelo_4.bugs')uranium <- unique(cbind(county, radon$Uppm))
u <- uranium[, 2]
radon_4_data <- list(n = n, J = J, y = y, county = county, x = x, u = u)
radon_4_inits <- function(){
list(a = rnorm(J), b = rnorm(1), g.0 = rnorm(1), g.1 = rnorm(1),
sigma.y = runif(1), sigma.a = runif(1))}
radon_4_parameters <- c("a", "b", "g.0", "g.1", "sigma.y", "sigma.a")
radon_4_jags <- jags(data = radon_4_data, inits= radon_4_inits,
parameters.to.save = radon_4_parameters, model.file = "modelo_4.bugs",
n.iter = 1000)
#> Compiling model graph
#> Resolving undeclared variables
#> Allocating nodes
#> Graph information:
#> Observed stochastic nodes: 919
#> Unobserved stochastic nodes: 90
#> Total graph size: 3258
#>
#> Initializing model
plot(radon_4_jags)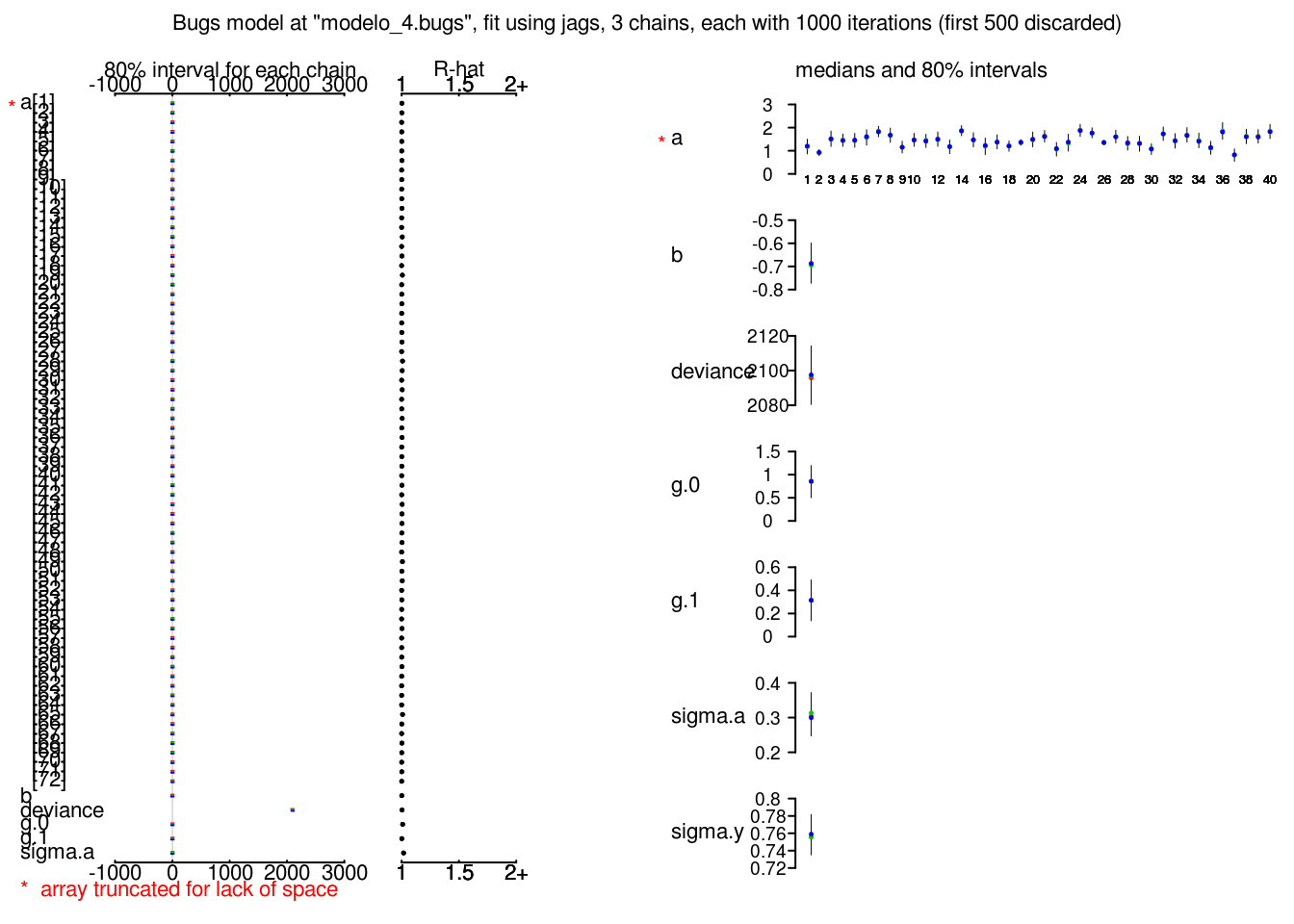
- Utiliza el modelo anterior para predecir el valor de radón para una nueva casa sin sótano (floor = 1) en el condado 26.
a26 <- radon_4_jags$BUGSoutput$sims.list$a[, 26]
b <- radon_4_jags$BUGSoutput$sims.list$b
sigma.y <- radon_4_jags$BUGSoutput$sims.list$sigma.y
n.sims <- length(b)
y_tilde <- rnorm(n.sims, a26 + b * 1, sigma.y)
sd_y_tilde <- sd(y_tilde)
# intervalo
c(mean(y_tilde) - 1.96 *sd_y_tilde, mean(y_tilde) + 1.96 *sd_y_tilde)
#> [1] -0.854 2.125- Utiliza el modelo anterior para predecir el valor de radón para una nueva casa sin sótano (floor = 1) en un condado nuevo con nivel de uranio \(2\).
g0 <- radon_4_jags$BUGSoutput$sims.list$g.0
g1 <- radon_4_jags$BUGSoutput$sims.list$g.1
sigma.a <- radon_4_jags$BUGSoutput$sims.list$sigma.a
a.new <- rnorm(n.sims, g0+g1, sigma.a)
y_tilde <- rnorm(n.sims, a.new + b * 1, sigma.y)
sd_y_tilde <- sd(y_tilde)
c(mean(y_tilde) - 1.96 * sd_y_tilde, mean(y_tilde) + 1.96 *sd_y_tilde)
#> [1] -1.15 2.11Referencias
Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Vol. Analytical methods for social research. New York: Cambridge University Press.