9.1 Máxima verosimilitud

El método más común para estimar parámetros es el método de máxima verosimilitud. Sea \(X_1,...,X_n\) independientes e idénticamente distribuidas con función de densidad de probabilidad \(p(x;\theta)\) entonces:

La función de verosimilitud se define como: \[\mathcal{L}(\theta) = \prod_{í=1}^n p(x_i;\theta).\] y la log-verosimilitud se define como \[\mathcal{l}(\theta)=\log \mathcal{L}(\theta)=\sum_{i=1}^n \log p(x_i; \theta)\]

La función de verosimilitud no es mas que la densidad conjunta de los datos, con la diferencia de que la tratamos como función del parámetro \(\theta\). Por tanto \(\mathcal{L}:\Theta \to [0, \infty)\), en general \(\mathcal{L}(\theta)\) no integra uno respecto a \(\theta\).

El estimador de máxima verosimilitud es el valor de \(\theta\) que maximiza \(\mathcal{L}(\theta)\).

El máximo de \(\mathcal{l}(\theta)\) se alcanza en el mismo lugar que el máximo de \(\mathcal{L}(\theta)\), por lo que maximizar la log-verosimilitud es equivalente a maximizar la verosimilitud.

Ejemplo: Bernoulli. Supongamos \(X_1,...X_n \sim Bernoulli(\theta)\). La función de densidad correspondiente es \(p(x;\theta)=\theta^x(1-\theta)^{1-x}\), por lo que:

\[\mathcal{L}(p)=\prod_{i=1}^n p(x_i;\theta)=\prod_{i=1}^n \theta^{x_i}(1-\theta)^{1-x_i}=\theta^{\sum x_i}(1-\theta)^{n-\sum x_i}\]

denotemos \(S=\sum x_i\), entonces \[\mathcal{l}(\theta)=S \log \theta + (n-S) \log (1-\theta)\] .

Si \(n=20\) y \(S=12\) tenemos la función:

# Verosimilitud X_1,...,X_n ~ Bernoulli(theta)
L_bernoulli <- function(n, S){
    function(theta){
        theta ^ S * (1 - theta) ^ (n - S)
    }  
}
# log-verosimilitud
l_bernoulli <- function(n, S){
    function(theta){
        S * log(theta) + (n - S) * log(1 - theta)
    }  
}
xy <- data.frame(x = 0:1, y = 0:1)
verosimilitud <- ggplot(xy, aes(x = x, y = y)) +
    stat_function(fun = L_bernoulli(n = 20, S = 12)) +
    xlab(expression(theta)) +
    ylab(expression(L(theta))) +
    ggtitle("Verosimilitud (n=20, S = 12)")

log_verosimilitud <- ggplot(xy, aes(x = x, y = y)) +
    stat_function(fun = l_bernoulli(n = 20, S = 12))+
    xlab(expression(theta)) +
    ylab(expression(l(theta))) +
    ggtitle("log-verosimilitud (n=20, S = 12)")

grid.arrange(verosimilitud, log_verosimilitud, nrow = 1)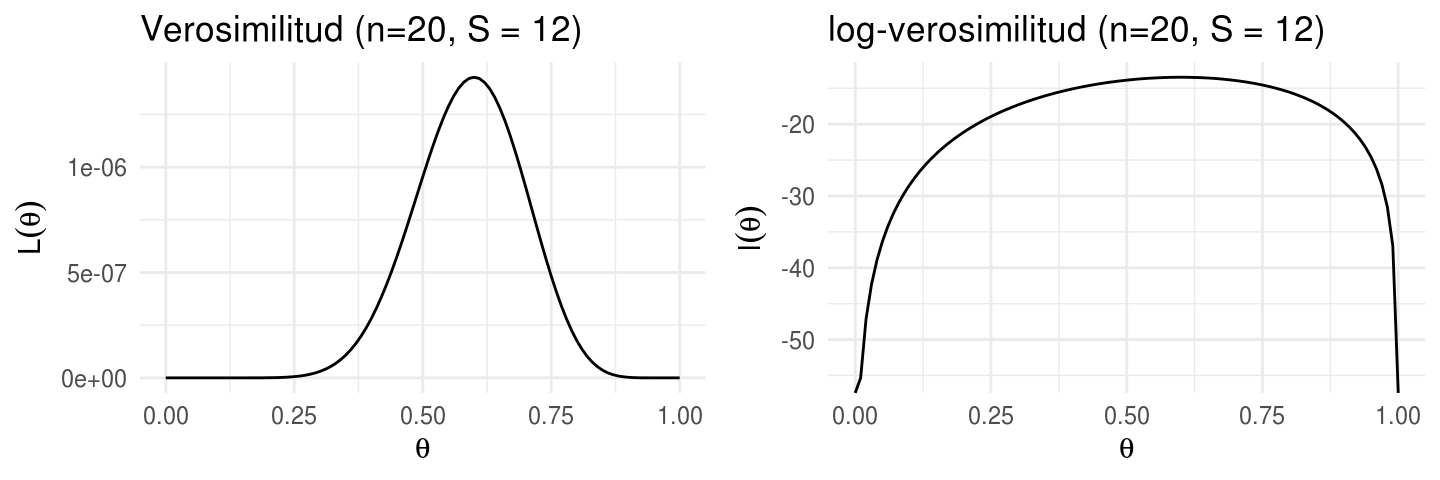

En ocasiones podemos calcular el estimador de máxima verosimilitud analíticamente, esto es derivando respecto al vector de parámetros de interés, igualando a cero el sistema de ecuaciones resultante, y revisando la segunda derivada para asegurar que se encontró un máximo. En el ejemplo este proceso lleva a \(\hat{\theta}=S/n\), y con \(S=12, n = 20\) obtenemos \(\hat{\theta}=0.6\).

Es muy común recurrir a métodos numéricos (por ejemplo Newton Raphson, BHHH, DFP) en el caso de R podemos usar las funciones optim u optimize.

optimize(L_bernoulli(n = 20, S = 12), interval = c(0, 1), maximum = TRUE)
#> $maximum
#> [1] 0.6
#> 
#> $objective
#> [1] 1.43e-06
optimize(l_bernoulli(n = 20, S = 12), interval = c(0, 1), maximum = TRUE)
#> $maximum
#> [1] 0.6
#> 
#> $objective
#> [1] -13.5

Sean \(X_1,...X_n \sim N(\mu, \sigma^2)\).

Calcula el estimador de máxima verosimilitud para \(\theta = (\mu, \sigma^2)\). Supongamos que observamos una muestra de tamaño \(100\) tal que: \(\sum X_i = 40\) y \(\sum X_i^2 = 20\).
Calcula \(\hat{\theta}\) usando el método de máxima verosimilitud.
¿Cómo graficarías la verosimilitud o log-verosimilitud?

Propiedades de los estimadores de máxima verosimilitud

Bajo ciertas condiciones del modelo, el estimador de máxima verosimilitud \(\hat{\theta}\) tiene propiedades deseables, las principales son:

Consistencia: \(\hat{\theta} \xrightarrow{P} \theta\) (converge en probabilidad), donde \(\theta\) es el verdadero valor del parámetro.
Equivariante: Si \(\hat{\theta}\) es el estimador de máxima verosimilitud de \(\theta\), entonces \(g(\hat{\theta})\) es el estimador de máxima verosimilitud de \(g(\theta)\).

Supongamos \(g\) invertible, entonces \(\hat{\theta} = g^{-1}(\hat{\eta})\). Para cualquier \(\eta\), \[\mathcal{L}(\eta)=\prod_{i=1}^n p(x_i;g^{-1}(\eta)) = \prod_{i=1}^n p(x_i;\theta)=\mathcal{L}(\theta)\] Por lo tanto, para cualquier \(\eta\), \[\mathcal{L}(\eta)=\mathcal{L}(\theta) \leq \mathcal{L}(\hat{\theta})=\mathcal{L}(\hat{\eta})\] y concluimos que \(\hat{\eta}=g(\hat{\theta})\) maximiza \(\mathcal{L}(\eta)\).

Ejemplo: Binomial. El estimador de máxima verosimilitud es \(\hat{p}=\bar{X}\). Si \(\eta=log(p/(1-p)\), entonces el estimador de máxima verosimilitud es \(\hat{\eta}=log(\hat{p}/(1-\hat{p}))\)

Asintóticamente normal: \(\hat{\theta} \leadsto N(\theta, I(\theta)^{-1})\), veremos a que nos referimos con \(I(\theta)^{-1}\) en la siguiente sección.

sim_sigma_hat <- function(n = 50, mu_sim = 0, sigma_sim = 1){
    x <- rnorm(n, mu_sim, sigma_sim)
    sigma_hat <- sqrt(sum((x - mean(x)) ^ 2) / n)
}

sigma_hats <- rerun(1000, sim_sigma_hat(n = 5, mu_sim = 10, sigma_sim = 5)) %>% 
    flatten_dbl()

# aprox normal con media theta y error estándar 
mean(sigma_hats)
#> [1] 4.24
sd(sigma_hats)
#> [1] 1.52

ggplot(data_frame(sigma_hats), aes(sample = sigma_hats)) +
    stat_qq() +
    stat_qq_line()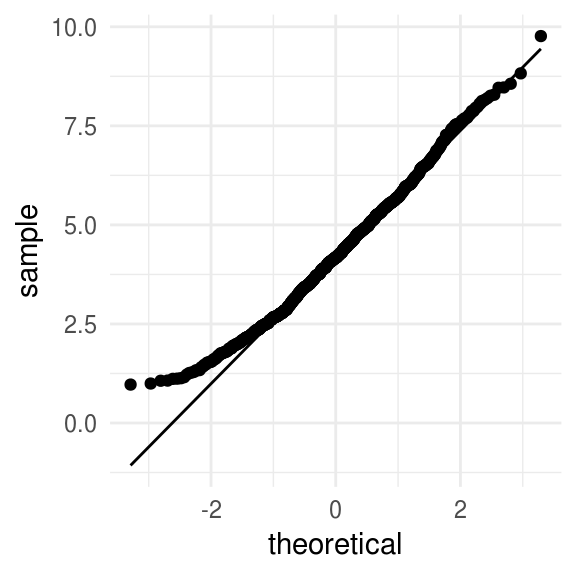

Asintóticamente eficiente: A grandes razgos, esto quiere decir que del conjunto de estimadores con comportamiento estable, el estimador de máxima verosimilitud tiene la menor varianza al menos para muestras grandes (alcanza la cota de Cramer-Rao).

Ahora que tenemos estimadores de maxima verosimilitud resta calcular errores estándar.

9.1.0.1 Matriz de información y errores estándar

La varianza de un estimador de máxima verosimilitud se calcula mediante la inversa de la matriz de información:

\[var(\theta)=[I_n(\theta)]^{-1}\]

La matriz de información es el negativo del valor esperado de la matriz Hessiana:

\[[I_n(\theta)] = - E[H(\theta)]\]

Y la Hessiana es la matriz de segundas derivadas de la log-verosimilitud respecto a los parámetros:

\[H(\theta)=\frac{d^2 \mathcal{l}(\theta)}{d\theta d\theta^´}\]

Entonces, la matriz de varianzas y covarianzas de \(\hat{\theta}\) es: \[var(\theta) = [I_n(\theta)]^{-1} = \big(-E[H(\theta)\big)^{-1}=\bigg(-E\bigg[\frac{d^2 \mathcal{l}(\theta)}{d\theta d\theta^´}\bigg]\bigg)^{-1}\]

En el caso Bernoulli obtenemos \(I_n(\theta) = \frac{n}{\theta(1-\theta)}\).

¿Porqué se calculan de esta manera los errores estándar? Idea intuitiva: Podemos pensar que la curvatura de la función de verosimilitud nos dice que tanta certeza tenemos de la estimación de nuestros parámetros. Entre más curva es la función de verosimilitud mayor es la certeza de que hemos estimado el parámetro adecuado. La segunda derivada de la verosimilitud es una medida de la curvatura local de la misma, es por esto que se utiliza para estimar la incertidumbre con la que hemos estimado los parámetros.

l_b1 <- ggplot(xy, aes(x = x, y = y)) +
    stat_function(fun = L_bernoulli(n = 20, S = 10)) +
    xlab(expression(theta)) +
    ylab(expression(L(theta))) +
    labs(title = "Verosimilitud", subtitle = "n=20, S = 10")
l_b2 <- ggplot(xy, aes(x = x, y = y)) +
    stat_function(fun = L_bernoulli(n = 20, S = 14)) +
    xlab(expression(theta)) +
    ylab(expression(L(theta))) +
    labs(title = "Verosimilitud", subtitle = "n=20, S = 14")
l_b3 <- ggplot(xy, aes(x = x, y = y)) +
    stat_function(fun = L_bernoulli(n = 20, S = 19)) +
    xlab(expression(theta)) +
    ylab(expression(L(theta))) +
    labs(title = "Verosimilitud", subtitle = "n=20, S = 19")

grid.arrange(l_b1, l_b2, l_b3, nrow = 1)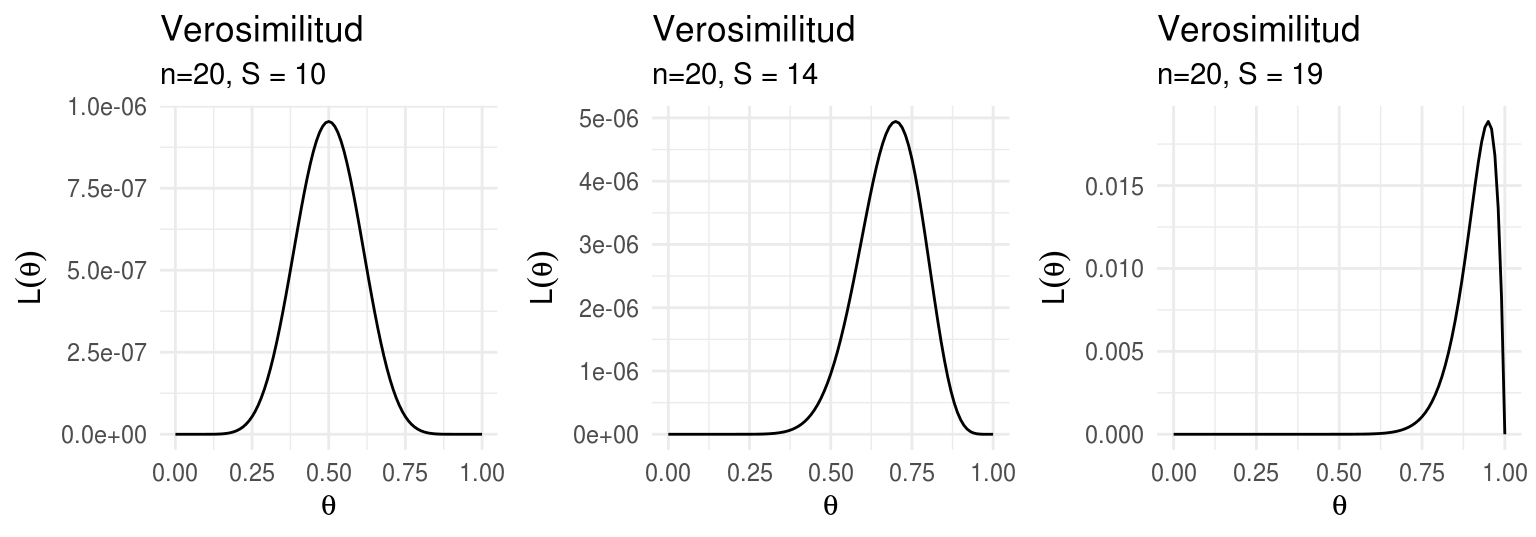

Adicionalmente, resulta que el estimador de máxima verosimilitud \(\hat{\theta}\) es aproximadamente Normal por lo que obtenemos el siguiente resultado

Bajo condiciones de regularidad apropiadas, se cumple:

Definimos \(se=\sqrt{1/I_n(\theta)}\), entonces \[\frac{(\hat{\theta} - \theta)}{se} \leadsto N(0, 1)\]
Definimos \(\hat{se}=\sqrt{1/I_n(\hat{\theta})}\), entonces \[\frac{(\hat{\theta} - \theta)}{\hat{se}} \leadsto N(0, 1)\]

El primer enunciado dice que \(\hat{\theta} \approx N(\theta,se)\), donde el error estándar de \(\hat{\theta}\) es \(se=\sqrt{1/I_n(\theta)}\). Por su parte el segundo enunciado dice que esto es cierto incluso si reemplazamos el error estándar por su aproximación \(\hat{se}=\sqrt{1/I_n(\hat{\theta})}\). Y podemos usar esto para construir intervalos de confianza.

Ejemplo: Bernoulli. Supongamos \(X_1,...X_n \sim Bernoulli(\theta)\). El estimador de máxima verosimilitud es \(\hat{\theta}=\sum X_i/n\) y un intervalo de aproximadamante \(95\%\) de confianza es: \[\hat{\theta} \pm 1.96 \bigg\{\frac{\hat{\theta}(1- \hat{\theta})}{n} \bigg\}^{1/2}\]

Método delta. Si \(\tau=g(\theta)\) donde \(\theta\) consta de únicamente un parámetro, \(g\) es diferenciable y \(g´(\theta)\neq 0\) entonces \[\frac{\sqrt{n}(\hat{\tau}-\tau)}{\hat{se}(\hat{\tau})}\leadsto N(0, 1)\] donde \(\hat{\tau}=g(\theta)\) y

\[\hat{se}(\hat{\tau})=|g´(\hat{\theta})|\hat{se}(\hat{\theta})\]

Por tanto, el método delta nos da una método para aproximar el error estándar y crear intervalos de confianza aproximados. Existe también una extensión del método delta para el caso en que \(\theta\) es un vector de dimensión mayor a uno, es decir cuando el modelo tiene más de un parámetro.

Notemos que los errores estándar de máxima verosimilutud son asintóticos, en el caso de tener muestras chicas podemos utilizar bootstrap para calcular errores estándar. Incluso con muestras grandes puede ser más conveniente usar Bootstrap pues nos permite calcular errores estándar cuando no hay fórmulas analíticas.