7.2 Variables aleatorias
El segundo requisito práctico de un proyecto de simulación es:
- Transformar los números aleatorios en variables de entrada del modelo (e.g. generación de muestras con cierta distribución).
En nuestro caso, usamos simulación aplicada a modelos estadísticos:
Un modelo estadístico \(F\) es un conjuto de distribuciones (o densidades o funciones de regresión). Un modelo paramétrico es un conjunto \(F\) que puede ser parametrizado por un número finito de parámetros.
Por ejemplo, si suponemos que los datos provienen de una distribución Normal, el modelo es:
\[F=\bigg\{p(x;\mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}exp\bigg(-\frac{1}{2\sigma^2}(x-\mu)^2\bigg), \mu \in \mathbb{R}, \sigma>0\bigg\}\]
En general, un modelo paramétrico tiene la forma
\[F=\bigg\{p(x;\theta):\theta \in \Theta \bigg\}\]
donde \(\theta\) es un parámetro desconocido (o un vector de parámetros) que puede tomar valores en el espacio paramétrico \(\Theta\).
En lo que resta de esta sección estudiaremos simulación de modelos paramétricos. Comencemos repasando algunos conceptos:
Una variable aleatoria es un mapeo entre el espacio de resultados y los números reales.
Ejemplo. Lanzamos una moneda justa dos veces, definimos \(X\) como en el número de soles, entonces la variable aleatoria se pueden resumir como:
| \(\omega\) | \(P(\{\omega\})\) | \(X(\omega)\) |
|---|---|---|
| AA | 1/4 | 0 |
| AS | 1/4 | 1 |
| SA | 1/4 | 1 |
| SS | 1/4 | 2 |
La función de distribución acumulada es la función \(P_X:\mathbb{R}\to[0,1]\) definida como: \[P_X(x)=P(X\leq x)\]
En el ejemplo: \[ P_X(x) = \left\{ \begin{array}{lr} 0 & x < 0\\ 1/4 & 0 \leq x < 1 \\ 3/4 & 1 \leq x < 2 \\ 1 & x \ge 2 \end{array} \right. \]
Una variable aleatoria \(X\) es discreta si toma un número contable de valores \(\{x_1,x_2,...\}\). En este caso definimos la función de probabilidad o la función masa de probabilidad de X como \(p_X(x)=P(X=x)\).
Notemos que \(p_X(x)\geq 0\) para toda \(x \in \mathbb{R}\) y \(\sum_i p_X(x)=1\). Más aún, la función de distribución acumulada esta relacionada con \(p_X\) por \[P_X(x)=P(X \leq x)= \sum_{x_i\leq x} = \sum_{x_i\leq x}p_{X}(x_i)\]
\[ p_X(x) = \left\{ \begin{array}{lr} 1/4 & x = 0 \\ 1/2 & x = 1 \\ 1/4 & x = 2\\ 0 & e.o.c. \end{array} \right. \]
Sea \(X\) una variable aleatoria con FDA \(P_X\). La función de distribución acumulada inversa o función de cuantiles se define como: \[P_X^{-1}(q) = inf\{x:P_X(x)>q\}\] para \(q \in [0,1]\).
Llamamos a \(P^{-1}(1/4)\) el primer cuartil, a \(P^{-1}(1/2)\) la mediana y \(P^{-1}(3/4)\) el tercer cuartil.
Familias discretas importantes
Muchas variables aleatorias provienen de familias o tipos de experimentos similares lo que nos ahorra tener que determinar las funciones de distribución y sus propiedades cada vez.
Por ejemplo, el resultado de interés en muchos experimentos es un resultado que solo puede tomar dos valores: una moneda puede ser águila o sol, un persona puede estar empleada o desempleada, un transistor puede estar defectuoso o no,… La misma distribución de probabilidad que describe a una variable aleatoria que puede tomar el valor de \(1\) con probabilidad \(p\) y \(0\) con probabilidad \(q=1-p\), se conoce como distribución Bernoulli.
Distribución Bernoulli
Sea \(X\) la variable aleatoria que representa un lanzamiento de moneda, con \(P(X=1)=p\) y \(P(X=0)=1-p\) para alguna \(p\in[0,1].\) Decimos que \(X\) tiene una distribución Bernoulli (\(X \sim Bernoulli(p)\)), y su función de distribución es:
\[ p(x) = \left\{ \begin{array}{lr} p^x(1-p)^{1-x} & x \in \{0,1\}\\ 0 & e.o.c. \\ \end{array} \right. \]
\(E(X) = p, Var(X)=p(1-p)\)
Notemos que un experimento Bernoulli es una repetición del experimento que involucra solo dos posibles salidas. Es común que nos interese el resultado de la repetición de experimentos Bernoulli independientes, en este caso se usa la distribución Binomial.
Distribución Binomial
Supongamos que tenemos una moneda que cae en sol con probabilidad \(p\), para alguna \(p\in[0,1].\) Lanzamos la moneda \(n\) veces y sea \(X\) el número de soles. Suponemos que los lanzamientos son independientes, entonces la función de distribución es:
\[ p(x) = \left\{ \begin{array}{lr} {n \choose x}p^x(1-p)^{n-x} & x \in \{0,1,...,n\}\\ 0 & e.o.c. \\ \end{array} \right. \]
\(E(X) = np, Var(X)=np(1-p)\)
Si \(X_1 \sim Binomial(n_1, p)\) y \(X_2 \sim Binomial(n_2,p)\) entonces \(X_1 + X_2 \sim Binomial(n_1+n_2, p)\). En general la distribución binomial describe el comportamiento de una variable \(X\) que cuenta número de éxitos tal que: 1) el número de observaciones \(n\) esta fijo, 2) cada observación es independiente, 3) cada observación representa uno de dos posibles eventos (éxito o fracaso) y 3) la probabilidad de éxito \(p\) es la misma en cada observación.
densidades <- ggplot(data.frame(x = -1:20)) +
geom_point(aes(x = x, y = dbinom(x, size = 20, prob = 0.5), color = "n=20;p=0.5"),
show.legend = FALSE) +
geom_path(aes(x = x, y = dbinom(x, size = 20, prob = 0.5), color = "n=20;p=0.5"),
alpha = 0.6, linetype = "dashed", show.legend = FALSE) +
geom_point(aes(x = x, y = dbinom(x, size = 20, prob = 0.1), color = "n=20;p=0.1"),
show.legend = FALSE) +
geom_path(aes(x = x, y = dbinom(x, size = 20, prob = 0.1), color = "n=20;p=0.1"),
alpha = 0.6, linetype = "dashed", show.legend = FALSE) +
labs(color = "", y = "", title = "Distribución binomial")
dists <- ggplot(data_frame(x = -1:20), aes(x)) +
stat_function(fun = pbinom, args = list(size = 20, prob = 0.5),
aes(colour = "n=20;p=0.5"), alpha = 0.8) +
stat_function(fun = pbinom, args = list(size = 20, prob = 0.1),
aes(colour = "n=20;p=0.1"), alpha = 0.8) +
labs(y = "", title = "FDA", color = "")
grid.arrange(densidades, dists, ncol = 2, newpage = FALSE)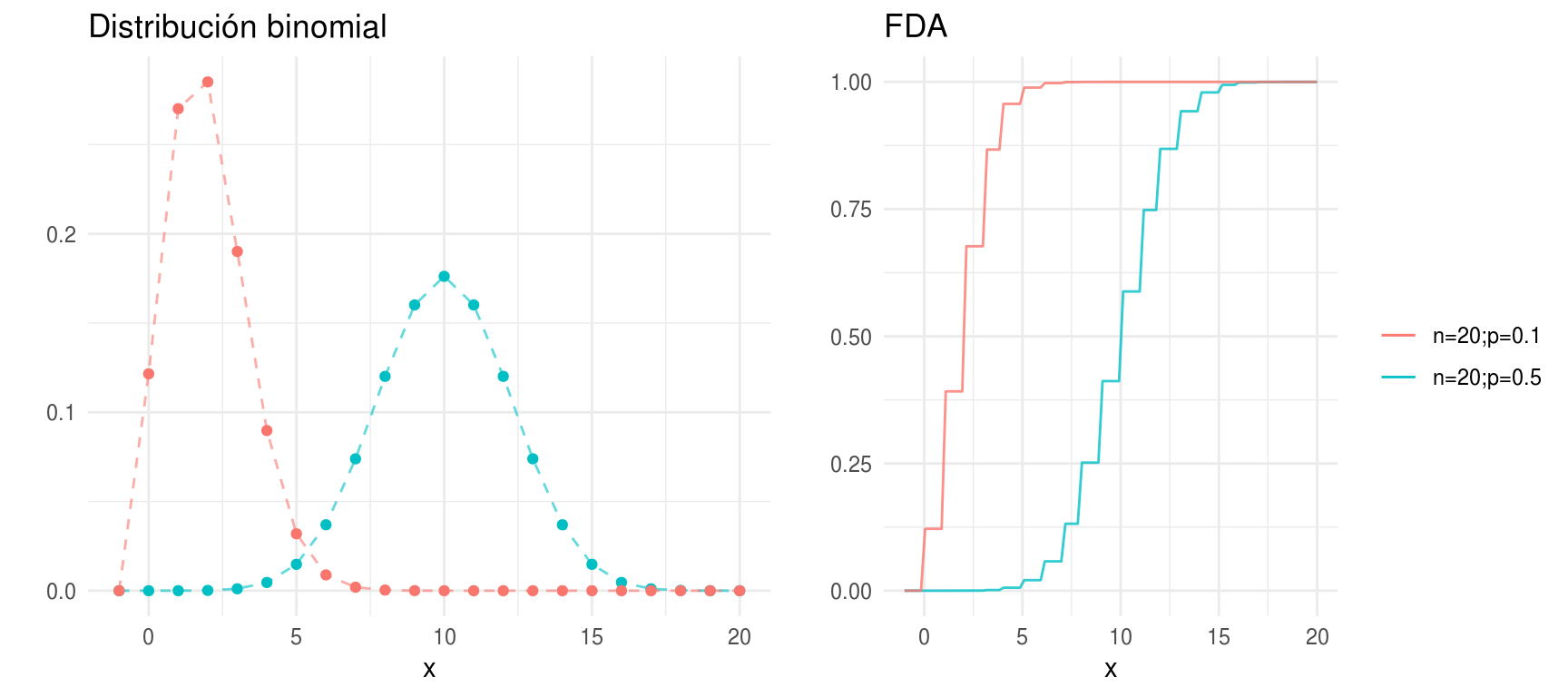
Distribución Uniforme
Decimos que \(X\) tiene una distribución uniforme en \(\{a,...,b\}\) (\(a,b\) enteros) si tiene una función de probailidad dada por:
\[ p(x) = \left\{ \begin{array}{lr} 1/n & x \in \{a,...,b\}\\ 0 & e.o.c. \\ \end{array} \right. \] donde \(n = b-a+1\), \(E(X) = (a+b)/2, Var(X)=(n^2-1)/12\)
El ejemplo más común es el lanzamiento de un dado.
Distribución Poisson
\(X\) tienen una distribución Poisson con parámetro \(\lambda\) si \[ p(x) = \left\{ \begin{array}{lr} e^{-\lambda} \frac{\lambda^x}{x!} & x \in \{0,1,...\}\\ 0 & e.o.c. \\ \end{array} \right. \]
\(E(X) = \lambda, Var(X)=\lambda\)
La distribución Poisson se utiliza con frecuencia para modelar conteos de eventos raros, por ejemplo número de accidentes de tráfico. La distribución Poisson es un caso límite de la distribución binomial cuando el número de casos es muy grande y la probabilidad de éxito \(p\) es chica.
Una propiedad de la distribución Poisson es: \(X_1 \sim Poisson(\lambda_1)\) y \(X_2 \sim Poisson(\lambda_2)\) entonces \(X_1 + X_2 \sim Poisson(\lambda_1 + \lambda_2)\).
densidades <- ggplot(data.frame(x = -1:20)) +
geom_point(aes(x = x, y = dpois(x, lambda = 4), color = "lambda=4"), show.legend = FALSE) +
geom_path(aes(x = x, y = dpois(x, lambda = 4), color = "lambda=4"),
alpha = 0.6, linetype = "dashed", show.legend = FALSE) +
geom_point(aes(x = x, y = dpois(x, lambda = 10), color = "lambda=10"), show.legend = FALSE) +
geom_path(aes(x = x, y = dpois(x, lambda = 10), color = "lambda=10"),
alpha = 0.6, linetype = "dashed", show.legend = FALSE) +
labs(color = "", y = "", title = "Distribución Poisson")
dists <- ggplot(data_frame(x = -1:20), aes(x)) +
stat_function(fun = ppois, args = list(lambda = 4),
aes(colour = "lambda=4"), alpha = 0.8) +
stat_function(fun = ppois, args = list(lambda = 10),
aes(colour = "lambda=10"), alpha = 0.8) +
labs(y = "", title = "FDA", color = "")
grid.arrange(densidades, dists, ncol = 2, newpage = FALSE)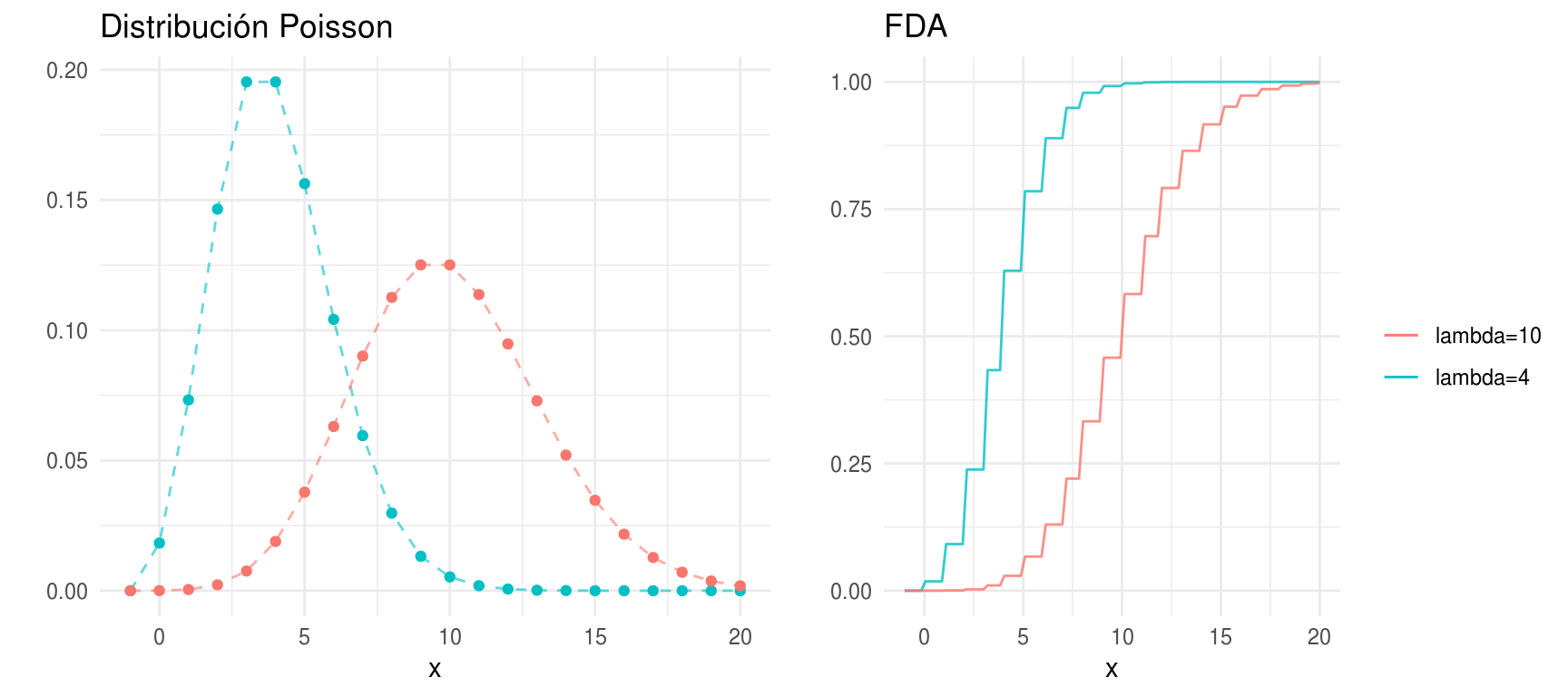
Distribución geométrica
\(X\) tiene distribución geométrica con parámetro \(p \in (0,1)\), \(X \sim Geom(p)\) si, \[ p(x) = \left\{ \begin{array}{lr} p(1-p)^{k-1} & x \in \{1,2,...\}\\ 0 & e.o.c. \\ \end{array} \right. \]
\(E(X)=1/p, Var(X)=(1-p)/p^2\)
con \(k \geq 1\). Podemos pensar en \(X\) como el número de lanzamientos necesarios
hasta que obtenemos el primer sol en los lanzamientos de una moneda.
densidades <- ggplot(data.frame(x = -1:20)) +
geom_point(aes(x = x, y = dgeom(x, p = 0.5), color = "p=0.5"), show.legend = FALSE) +
geom_path(aes(x = x, y = dgeom(x, p = 0.5), color = "p=0.5"), show.legend = FALSE,
alpha = 0.6, linetype = "dashed") +
geom_point(aes(x = x, y = dgeom(x, p = 0.1), color = "p=0.1"), show.legend = FALSE) +
geom_path(aes(x = x, y = dgeom(x, p = 0.1), color = "p=0.1"),
show.legend = FALSE, alpha = 0.6, linetype = "dashed") +
labs(title = "Distribución geométrica", y = "")
dists <- ggplot(data_frame(x = -1:20), aes(x)) +
stat_function(fun = pgeom, args = list(p = 0.5),
aes(colour = "p=0.5"), alpha = 0.8) +
stat_function(fun = pgeom, args = list(p = 0.1),
aes(colour = "p=0.1"), alpha = 0.8) +
labs(y = "", title = "FDA", color = "")
grid.arrange(densidades, dists, ncol = 2, newpage = FALSE)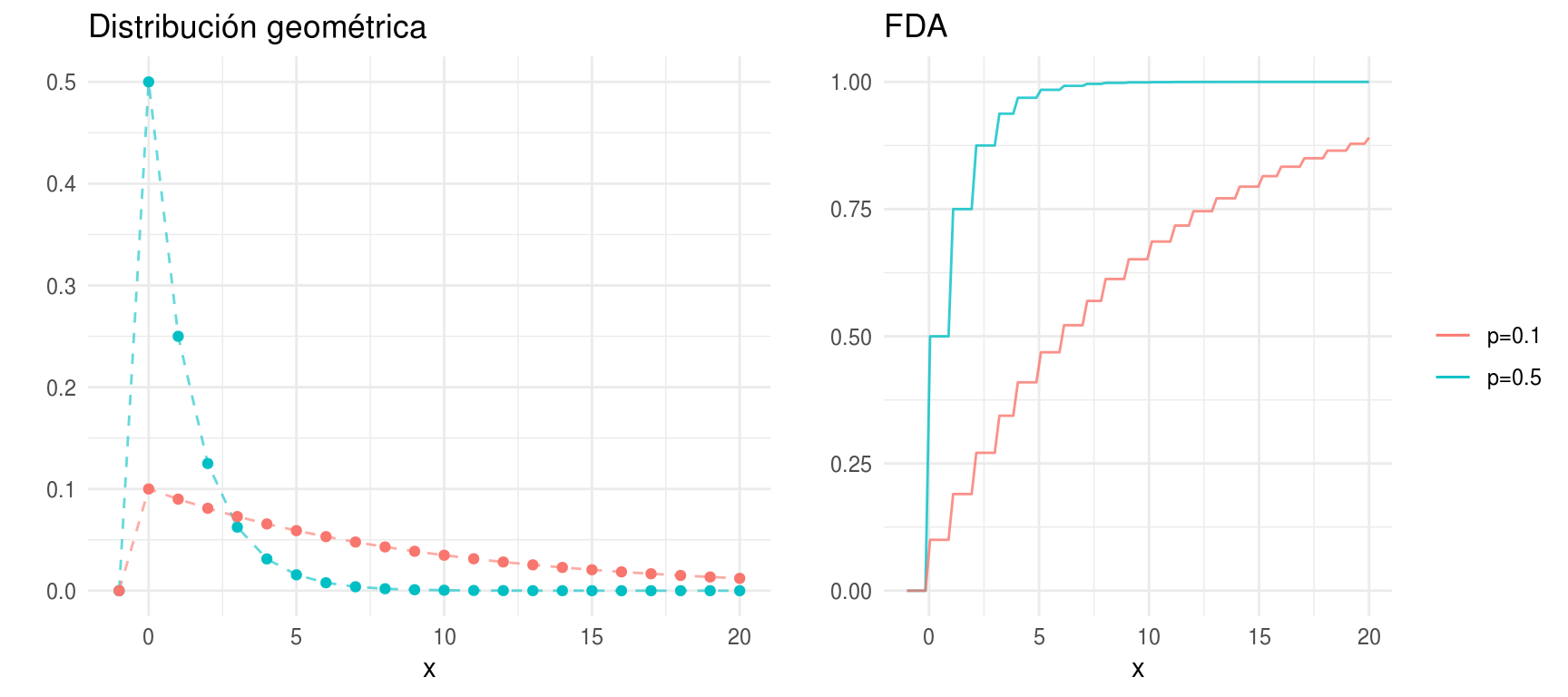
Variables aleatorias continuas
Una variable aleatoria \(X\) es continua si existe una función \(p_x\) tal que \(p_X(x) \geq 0\) para toda \(x\), \(\int_{-\infty}^{\infty}p_X(x)dx=1\) y para toda \(a\leq b\),
\[P(a < X < b) = \int_{a}^b p_X(x)dx\]
La función \(p_X(x)\) se llama la función de densidad de probabilidad (fdp). Tenemos que \[P_X(x)=\int_{-\infty}^x p_X(t)dt\] y \(p_X(x)=P_X^{\'}(x)\) en todos los puntos \(x\) en los que la FDA \(P_X\) es diferenciable.
Ejemplo. Supongamos que elegimos un número al azar entre cero y uno, entonces
\[ p(x) = \left\{ \begin{array}{lr} \frac{1}{b-a} & x \in [0, 1]\\ 0 & e.o.c. \\ \end{array} \right. \] es claro que \(p_X(x) \geq 0\) para toda \(x\) y \(\int_{-\infty}^{\infty}p_X(x)dx=1\), la FDA esta dada por
\[ P_X(x) = \left\{ \begin{array}{lr} 0 & x < 0 \\ x & x \in [0,1]\\ 1 & x>b \\ \end{array} \right. \]
Vale la pena notar que en el caso de variables aleatorias continuas \(P(X=x)=0\)
para toda \(x\) y pensar en \(p_X(x)\) como \(P(X=x)\) solo tiene sentido en el caso
discreto.
Familias Continuas importantes
Distribución Uniforme
\(X\) tiene una distribución \(Uniforme(a,b)\) si
\[ p(x) = \left\{ \begin{array}{lr} \frac{1}{b-a} & x \in [a,b]\\ 0 & e.o.c. \\ \end{array} \right. \]
donde \(a < b\). La función de distribución acumualda es
\[ P_X(x) = \left\{ \begin{array}{lr} 0 & x < a \\ \frac{x-a}{b-a} & x \in [a,b]\\ 1 & x>b \\ \end{array} \right. \]
\(E(X) = (a+b)/2, Var(X)= (b-a)^2/12\)
densidades <- ggplot(data_frame(x = c(-5 , 5)), aes(x)) +
stat_function(fun = dunif, aes(colour = "a=0; b=1"), show.legend = FALSE) +
stat_function(fun = dunif, args = list(min = -5, max = 5), aes(colour = "a=-5; b=5"), show.legend = FALSE) +
stat_function(fun = dunif, args = list(min = 0, max = 2), aes(colour = "a=0; b=2"), show.legend = FALSE) +
labs(y = "", title = "Distribución uniforme", colour = "")
dists <- ggplot(data_frame(x = c(-5 , 5)), aes(x)) +
stat_function(fun = punif, aes(colour = "a=0; b=1"), show.legend = FALSE) +
stat_function(fun = punif, args = list(min = -5, max = 5), aes(colour = "a=-5; b=5"), show.legend = FALSE) +
stat_function(fun = punif, args = list(min = 0, max = 2), aes(colour = "a=0; b=2"), show.legend = FALSE) +
labs(y = "", title = "FDA")
grid.arrange(densidades, dists, ncol = 3, newpage = FALSE)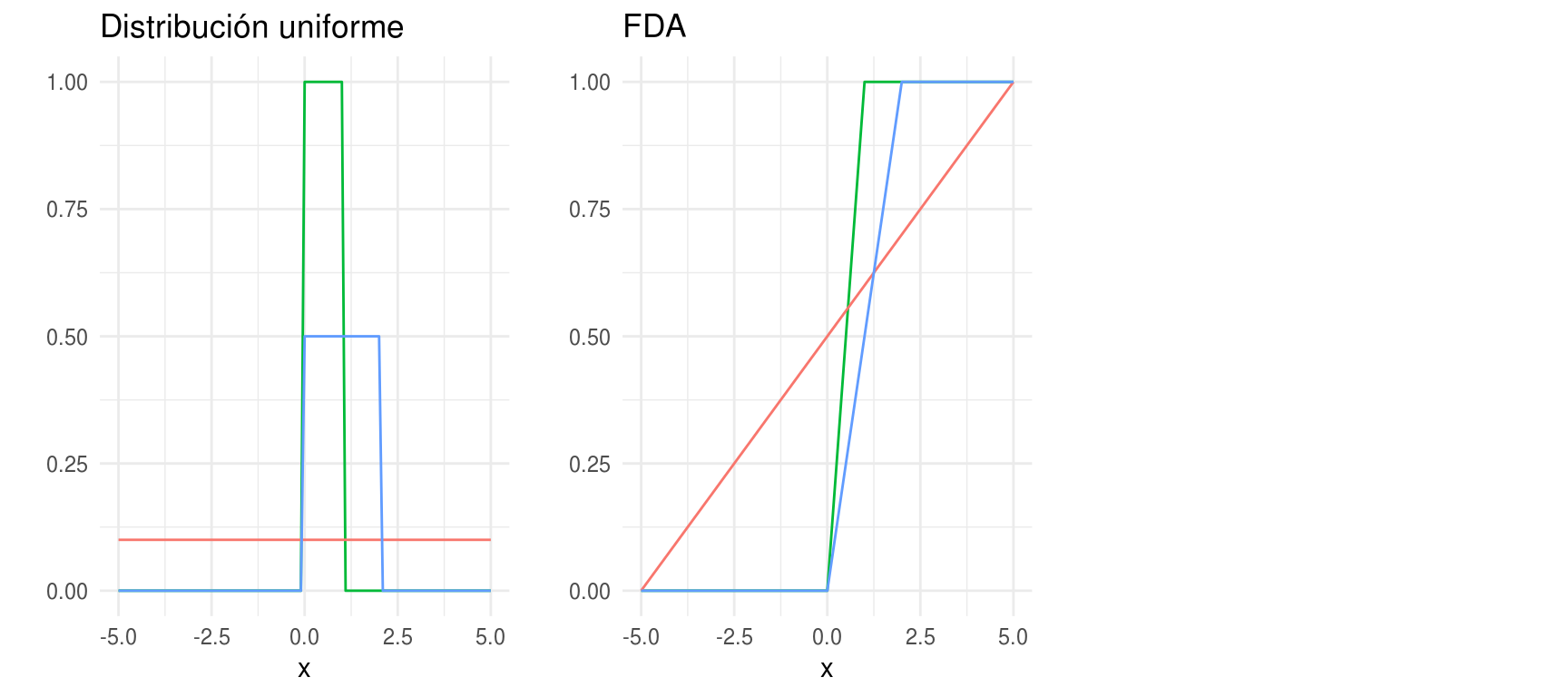
Distribución Normal
\(X\) tiene una distribución normal con parámetros \(\mu\) y \(\sigma\), denotado \(X\sim N(\mu, \sigma^2)\) si
\[p(x) = \frac{1}{\sigma\sqrt{2\pi}}exp\bigg(-\frac{1}{2\sigma^2}(x-\mu)^2\bigg)\]
\(E(X)=\mu, Var(X)=\sigma^2\)
donde \(\mu \in \mathbb{R}\) y \(\sigma>0\).
Decimos que \(X\) tiene una distribución Normal estándar si \(\mu=0\) y \(\sigma=1\). Una variable aleatoria Normal estándar se denota tradicionalmente por \(Z\), su función de densidad de probabilidad por \(\phi(z)\) y la función de probabilidad acumulada por \(\Phi(z)\).
Algunas porpiedades importantes son:
Si \(X \sim N(\mu, \sigma^2)\), entonces \(Z=(X-\mu)/\sigma \sim N(0,1)\).
Si \(Z \sim N(0, 1)\) entonces \(X = \mu + \sigma Z \sim N(\mu, sigma^2)\).
Si \(X_i \sim N(\mu_i, \sigma_i^2)\), \(i=1,...,n\) independientes, entonces: \[\sum_{i=1}^n X_i \sim N(\sum_{i=1}^n \mu_i, \sum_{i=1}^n \sigma_i^2)\]
Se sigue de 1 que si \(X\sim N(\mu, \sigma^2)\), entonces \[P(a<X<b) = P\big(\frac{a-\mu}{\sigma} < Z < \frac{b-\mu}{\sigma}\big)= \Phi\big(\frac{b-\mu}{\sigma}\big) - \Phi\big(\frac{a-\mu}{\sigma}\big)\]
densidades <- ggplot(data_frame(x = c(-5 , 5)), aes(x)) +
stat_function(fun = dnorm, aes(colour = "m=0; s=1"), show.legend = FALSE) +
stat_function(fun = dnorm, args = list(mean = 1), aes(colour = "m=1; s=1"), show.legend = FALSE) +
stat_function(fun = dnorm, args = list(sd = 2), aes(colour = "m=1; s=2"), show.legend = FALSE) +
labs(y = "", title = "Distribución Normal", colour = "")
dists <- ggplot(data_frame(x = c(-5 , 5)), aes(x)) +
stat_function(fun = pnorm, aes(colour = "m=0; s=1"), show.legend = FALSE) +
stat_function(fun = pnorm, args = list(mean = 1), aes(colour = "m=1; s=1"), show.legend = FALSE) +
stat_function(fun = pnorm, args = list(sd = 2), aes(colour = "m=1; s=2"), show.legend = FALSE) +
labs(y = "", title = "FDA")
cuantiles <- ggplot(data_frame(x = c(0, 1)), aes(x)) +
stat_function(fun = qnorm, aes(colour = "m=0; s=1")) +
stat_function(fun = qnorm, args = list(mean = 1), aes(colour = "m=1; s=1")) +
stat_function(fun = qnorm, args = list(sd = 2), aes(colour = "m=1; s=2")) +
labs(y = "", title = "Funciones de cuantiles", colour = "")
grid.arrange(densidades, dists, cuantiles, ncol = 3, newpage = FALSE)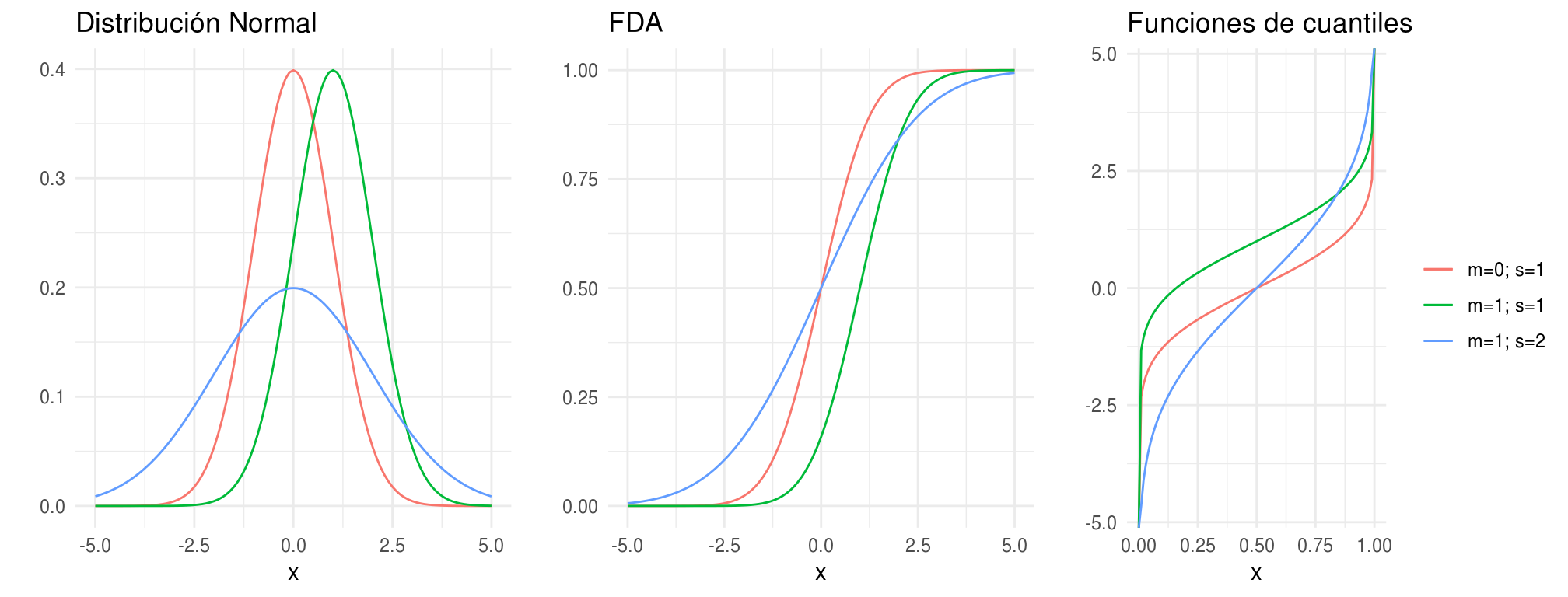
Distribución Exponencial
Una variable aleatoria \(X\) tienen distribución Exponencial con parámetro \(\beta\), \(X \sim Exp(\beta)\) si,
\[ p(x) = \left\{ \begin{array}{lr} \frac{1}{\beta}e^{-x/\beta} & x >0\\ 0 & e.o.c. \\ \end{array} \right. \]
\(E(X)=\beta, Var(X)=\beta^2\)
donde \(\beta > 0\). La distribución exponencial se utiliza para modelar tiempos de espera hasta un evento, por ejemplo modelar el tiempo de vida de un componente electrónico o el tiempo de espera entre llamadas telefónicas.
Distribución Gamma
Comencemos definiendo la función Gamma: para \(\alpha>0\), \(\Gamma(\alpha)=\int_0^{\infty}y^{\alpha-1}e^{-y}dy\), esta función es una extensión de la función factorial, tenemos que si \(n\) es un entero positivo, \(\Gamma(n)=(n-1)!\).
Ahora, \(X\) tienen una distribución Gamma con parámetros \(\alpha\), \(\beta\), denotado como \(X \sim Gamma(\alpha, \beta)\) si
\[
p(x) = \left\{
\begin{array}{lr}
\frac{1}{\beta^\alpha \Gamma(\alpha)}x^{\alpha-1}e^{-x/\beta} & x >0\\
0 & e.o.c. \\
\end{array}
\right.
\]
\(E(X)=\alpha \beta, Var(X)=\alpha \beta^2\)
Vale la pena notar que una distribución exponencial es una \(Gamma(1, \beta)\).
Una propiedad adicional es que si \(X_i \sim Gamma(\alpha_i, \beta)\) independientes, entonces \(\sum_{i=1}^n X_i \sim Gamma(\sum_{i=1}^n \alpha_i, \beta)\).
En la práctica la distribución Gamma se ha usado para modelar el tamaño de las reclamaciones de asegurados, en neurociencia se ha usado para describir la distribución de los intervalos entre los que ocurren picos. Finalmente, la distribución Gamma es muy usada en estadística bayesiana como a priori conjugada para el parámetro de precisión de una distribución Normal.
densidades <- ggplot(data_frame(x = c(0 , 12)), aes(x)) +
stat_function(fun = dgamma, args = list(shape = 1), aes(colour = "a=1;b=1"), show.legend = FALSE) +
stat_function(fun = dgamma, args = list(scale = 0.5, shape = 2), aes(colour = "a=2;b=0.5"), show.legend = FALSE) +
stat_function(fun = dgamma, args = list(scale = 3, shape = 4), aes(colour = "a=4,b=3"), show.legend = FALSE) +
labs(y = "", title = "Distribución Gamma", colour = "")
dists <- ggplot(data_frame(x = c(0 , 12)), aes(x)) +
stat_function(fun = dgamma, args = list(shape = 1), aes(colour = "a=1;b=1")) +
stat_function(fun = dgamma, args = list(scale = 0.5, shape = 2), aes(colour = "a=2;b=0.5")) +
stat_function(fun = dgamma, args = list(scale = 3, shape = 4), aes(colour = "a=4,b=3")) +
labs(y = "", title = "FDA", color="")
grid.arrange(densidades, dists, ncol = 2, newpage = FALSE)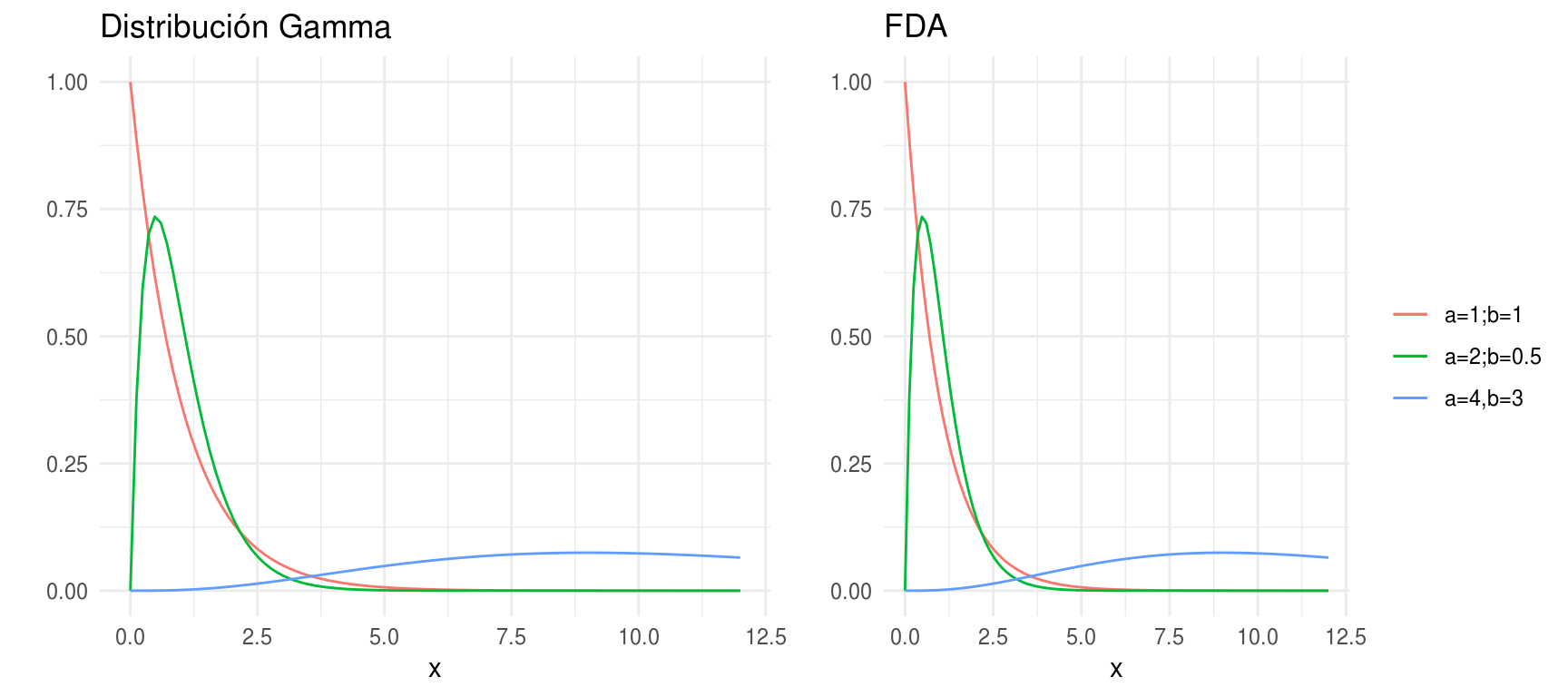
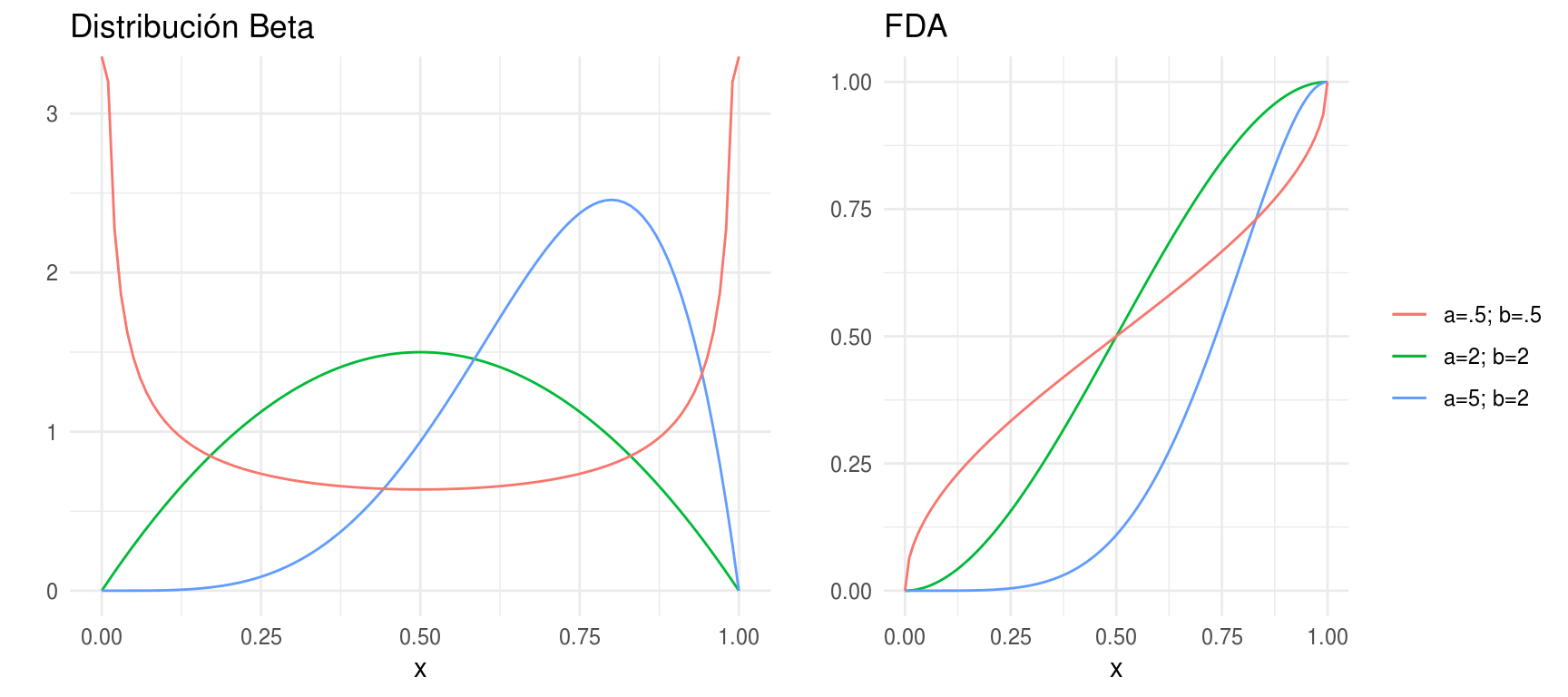
Distribución Beta
- \(X\) tiene una distrinución Beta con parámetros \(\alpha > 0\) y \(\beta >0\), \(X \sim Beta(\alpha, \beta)\) si
\[ p(x) = \left\{ \begin{array}{lr} \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1} & 0 < x < 1\\ 0 & e.o.c. \\ \end{array} \right. \] \(E(X)=\alpha/(\alpha+\beta), Var(X)=\alpha \beta /[(\alpha+\beta)^2(\alpha + \beta + 1)]\)
La distribución Beta se ha utilizado para describir variables aleatorias
limitadas a intervalos de longitud finita, por ejemplo, distribución del tiempo
en sistemas de control o administración de proyectos, proporción de minerales
en rocas, etc.
densidades <- ggplot(data_frame(x = c(0 , 1)), aes(x)) +
stat_function(fun = dbeta, args = list(shape1 = 2, shape2 = 2),
aes(colour = "a=2; b=2"), show.legend = FALSE) +
stat_function(fun = dbeta, args = list(shape1 = 5, shape2 = 2),
aes(colour = "a=5; b=2"), show.legend = FALSE) +
stat_function(fun = dbeta, args = list(shape1 = .5, shape2 = .5),
aes(colour = "a=.5; b=.5"), show.legend = FALSE) +
labs(y = "", title = "Distribución Beta", colour = "")
dists <- ggplot(data_frame(x = c(0 , 1)), aes(x)) +
stat_function(fun = pbeta, args = list(shape1 = 2, shape2 = 2),
aes(colour = "a=2; b=2")) +
stat_function(fun = pbeta, args = list(shape1 = 5, shape2 = 2),
aes(colour = "a=5; b=2")) +
stat_function(fun = pbeta, args = list(shape1 = .5, shape2 = .5),
aes(colour = "a=.5; b=.5")) +
labs(y = "", title = "FDA", color="")
grid.arrange(densidades, dists, ncol = 2, newpage = FALSE)