Sección 1 Introducción a visualización

“The simple graph has brought more information to the data analyst’s mind than any other device.” — John Tukey

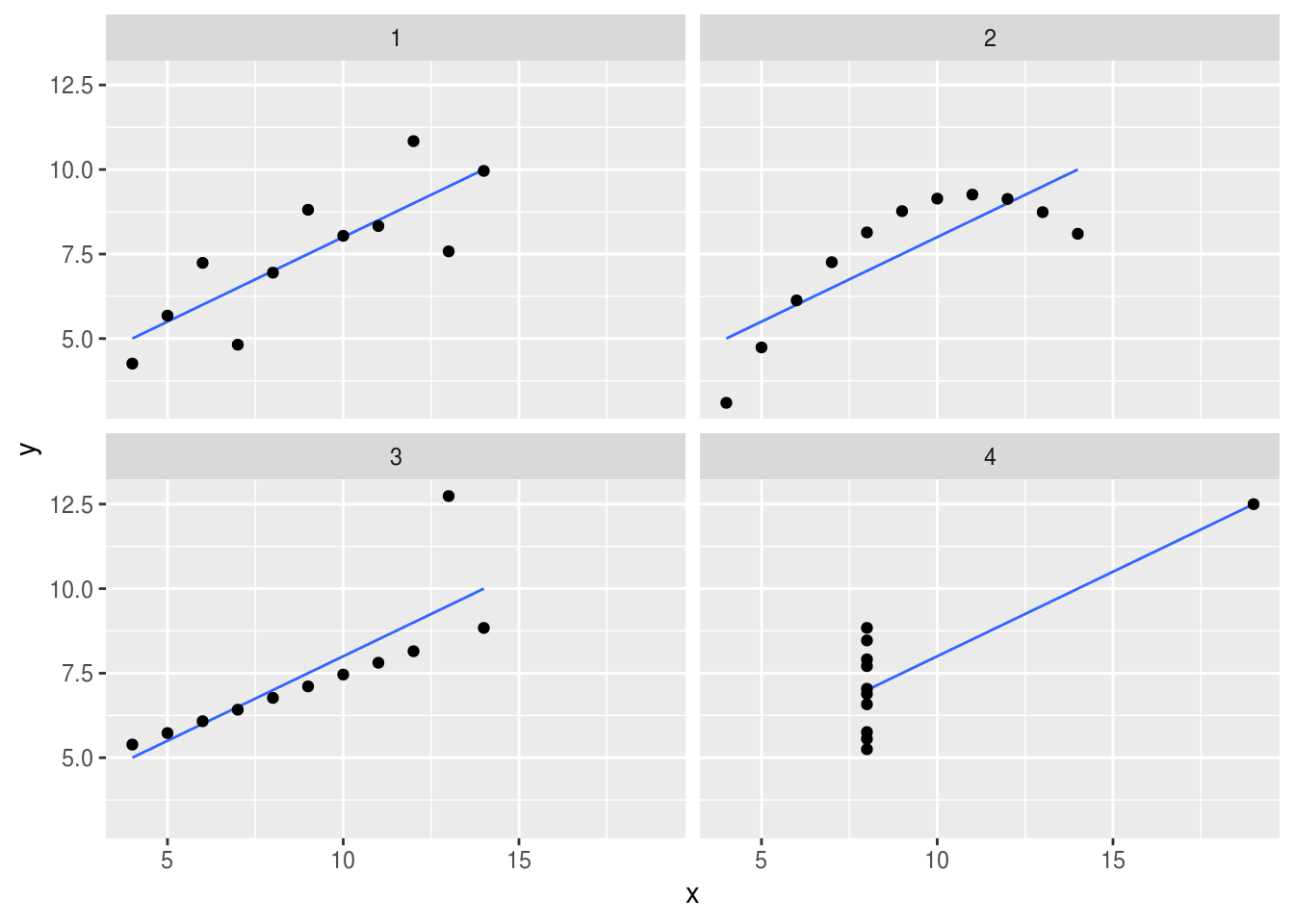
El cuarteto de Ascombe

En 1971 un estadístico llamado Frank Anscombe (fundador del departamento de Estadística de la Universidad de Yale) publicó cuatro conjuntos de datos, cada uno consiste de 11 observaciones y tienen las mismas propiedades estadísticas.

Sin embargo, cuando analizamos los datos de manera gráfica en un histograma encontramos rápidamente que los conjuntos de datos son muy distintos.

Media de \(x\): 9
Varianza muestral de \(x\): 11
Media de \(y\): 7.50
Varianza muestral de \(y\): 4.12
Correlación entre \(x\) y \(y\): 0.816
Línea de regresión lineal: \(y = 3.00 + 0.500x\)

En la gráfica del primer conjunto de datos, se ven datos como los que se tendrían en una relación lineal simple con un modelo que cumple los supuestos de normalidad. La segunda gráfica (arriba a la derecha) muestra unos datos que tienen una asociación pero definitivamente no es lineal. En la tercera gráfica (abajo a la izquierda) están puntos alineados perfectamente en una línea recta, excepto por uno de ellos. En la última gráfica podemos ver un ejemplo en el cual basta tener una observación atípica para que se produzca un coeficiente de correlación alto aún cuando en realidad no existe una asociación lineal entre las dos variables.

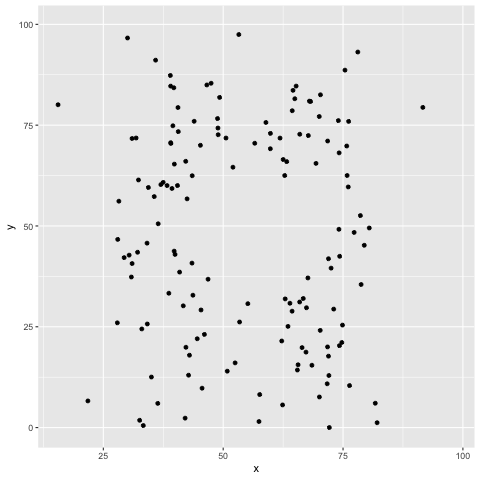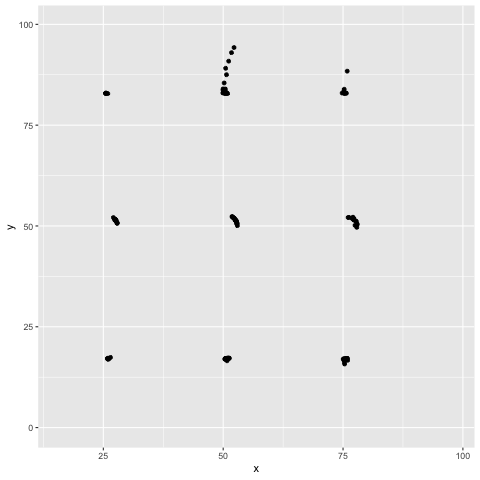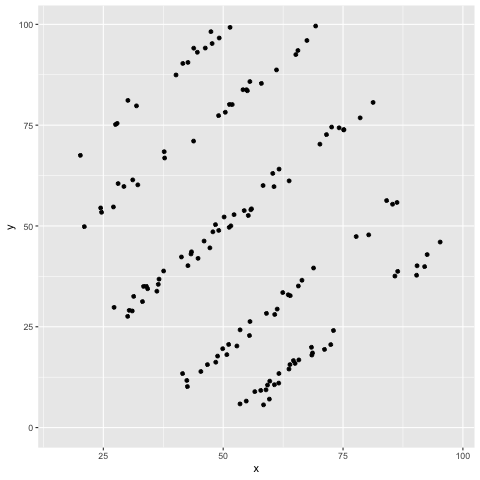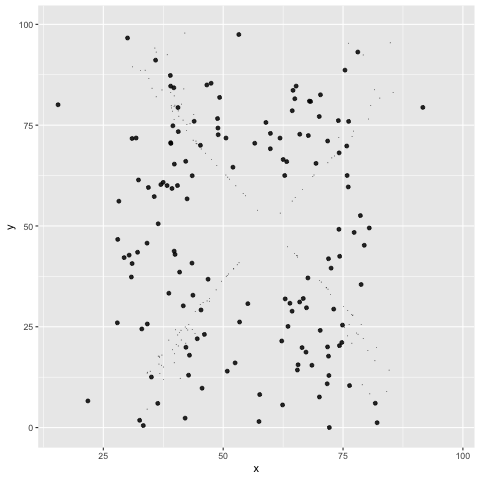
El cuarteto de Ascombe inspiró una técnica para crear datos que comparten las propiedades estadísticas al igual que en el cuarteto, pero que producen gráficas muy distintas (Matejka, Fitzmaurice).