11-Metropolis
Regresamos al ejercicio de IQ de la tarea anterior, en ésta hiciste cálculos para el caso de una sola observación. En este ejercicio consideramos el caso en que observamos una muestra \(x=\{x_1,...,x_N\}\), y utilizaremos Metrópolis para obtener una muestra de la distribución posterior.
- Crea una función \(prior\) que reciba los parámetros \(\mu\) y \(\tau\) que definen tus creencias del parámetro desconocido \(\theta\) y devuelva \(p(\theta)\), donde \(p(\theta)\) tiene distriución \(N(\mu, \sigma^2)\)
prior <- function(mu, tau{
function(theta){
... # llena esta parte
}
}- Utiliza la función que acabas de escribir para definir una distribución inicial con parámetros \(\mu = 150\) y \(\tau = 15\), llámala mi_prior.
Ya que tenemos la distribución inicial debemos escribir la verosimilitud, en este caso la verosimilitud es:
\[p(x|\theta, \sigma^2)=\frac{1}{(2\pi\sigma^2)^{N/2}}exp\left(-\frac{1}{2\sigma^2}\sum_{j=1}^{N}(x_j-\theta)^2\right)\] \[=\frac{1}{(2\pi\sigma^2)^{N/2}}exp\left(-\frac{1}{2\sigma^2}\bigg(\sum_{j=1}^{N}x_j^2-2\theta\sum_{j=1}^{N} x_j + N\theta^2 \bigg) \right)\]
Recuerda que estamos suponiendo varianza conocida, supongamos que la desviación estándar es \(\sigma=20\).
\[p(x|\theta)=\frac{1}{(2\pi (20^2))^{N/2}}exp\left(-\frac{1}{2 (20^2)}\bigg(\sum_{j=1}^{N}x_j^2-2\theta\sum_{j=1}^{N} x_j + N\theta^2 \bigg) \right)\]
- Crea una función \(likeNorm\) en R que reciba la desviación estándar, la suma de los valores observados \(\sum x_i\), la suma de los valores al cuadrado \(\sum x_i^2\) y el número de observaciones \(N\) la función devolverá la función de verosimilitud (es decir va a regresar una función que depende únicamente de \(\theta\)).
# S: sum x_i, S2: sum x_i^2, N: número obs.
likeNorm <- function(S, S2, N){
function(theta){
... # llena esta parte
}
}Supongamos que aplicamos un test de IQ a \(100\) alumnos y observamos que la suma de los puntajes es \(13,300\), es decir \(\sum x_i=13,000\) y \(\sum x_i^2=1,700,000\). Utiliza la función que acabas de escribir para definir la función de verosimilitud condicional a los datos observados, llámala mi_like.
La distribución posterior no normalizada es simplemente el producto de la inicial y la posterior:
postRelProb <- function(theta){
mi_like(theta) * mi_prior(theta)
}Utiliza Metropolis para obtener una muestra de valores representativos de la distribución posterior de \(\theta\). Para proponer los saltos utiliza una \(Normal(0, 5)\).
Grafica los valores de la cadena para cada paso.
Elimina los valores correspondientes a la etapa de calentamiento y realiza un histograma de la distribución posterior.
Si calcularas la posterior de manera analítica obtendrías que \(p(x|\theta)\) es normal con media: \[\frac{\sigma^2}{\sigma^2 + N\tau^2}\mu + \frac{N\tau^2}{\sigma^2 + N \tau^2}\bar{x}\] y varianza \[\frac{\sigma^2 \tau^2}{\sigma^2 + N\tau^2}\]
donde \(\bar{x}=1/N\sum_{i=1}^N x_i\) es la media de los valores observados. Realiza simulaciones de la distribución posterior calculada de manera analítica y comparalas con el histograma de los valores generados con Metropolis.
- ¿Cómo utilizarías los parámetros \(\mu, \tau^2\) para describir un escenario donde sabes poco del verdadero valor de la media \(\theta\)?
Solución
prior <- function(mu = 100, tau = 10){
function(theta){
dnorm(theta, mu, tau)
}
}
mu <- 150
tau <- 15
mi_prior <- prior(mu, tau)# S: sum x_i, S2: sum x_i^2, N: número obs., sigma: desviación estándar (conocida)
S <- 13000
S2 <- 1700000
N <- 100
# sigma2 <- S2 / N - (S / N) ^ 2
sigma <- 20
likeNorm <- function(S, S2, N, sigma = 20){
# quitamos constantes
sigma2 <- sigma ^ 2
function(theta){
exp(-1 / (2 * sigma2) * (S2 - 2 * theta * S +
N * theta ^ 2))
}
}mi_like <- likeNorm(S = S, S2 = S2, N = N, sigma = sigma)
mi_like(130)
#> [1] 3.73e-06postRelProb <- function(theta){
mi_like(theta) * mi_prior(theta)
}
# para cada paso decidimos el movimiento de acuerdo a la siguiente función
caminaAleat <- function(theta, sd_prop = 5){ # theta: valor actual
salto_prop <- rnorm(n = 1, sd = sd_prop) # salto propuesto
theta_prop <- theta + salto_prop # theta propuesta
u <- runif(1)
p_move = min(postRelProb(theta_prop) / postRelProb(theta), 1) # prob mover
if(p_move > u){
return(theta_prop) # aceptar valor propuesto
}
else{
return(theta) # rechazar
}
}
pasos <- 10000
camino <- numeric(pasos) # vector que guardará las simulaciones
camino[1] <- 90 # valor inicial
rechazo = 0
# Generamos la caminata aleatoria
for (j in 2:pasos){
camino[j] <- caminaAleat(camino[j - 1])
rechazo <- rechazo + 1 * (camino[j] == camino[j - 1])
}
rechazo / pasos
#> [1] 0.583
caminata <- data.frame(pasos = 1:pasos, theta = camino)ggplot(caminata[1:2000, ], aes(x = pasos, y = theta)) +
geom_point(size = 0.8) +
geom_path(alpha = 0.3) 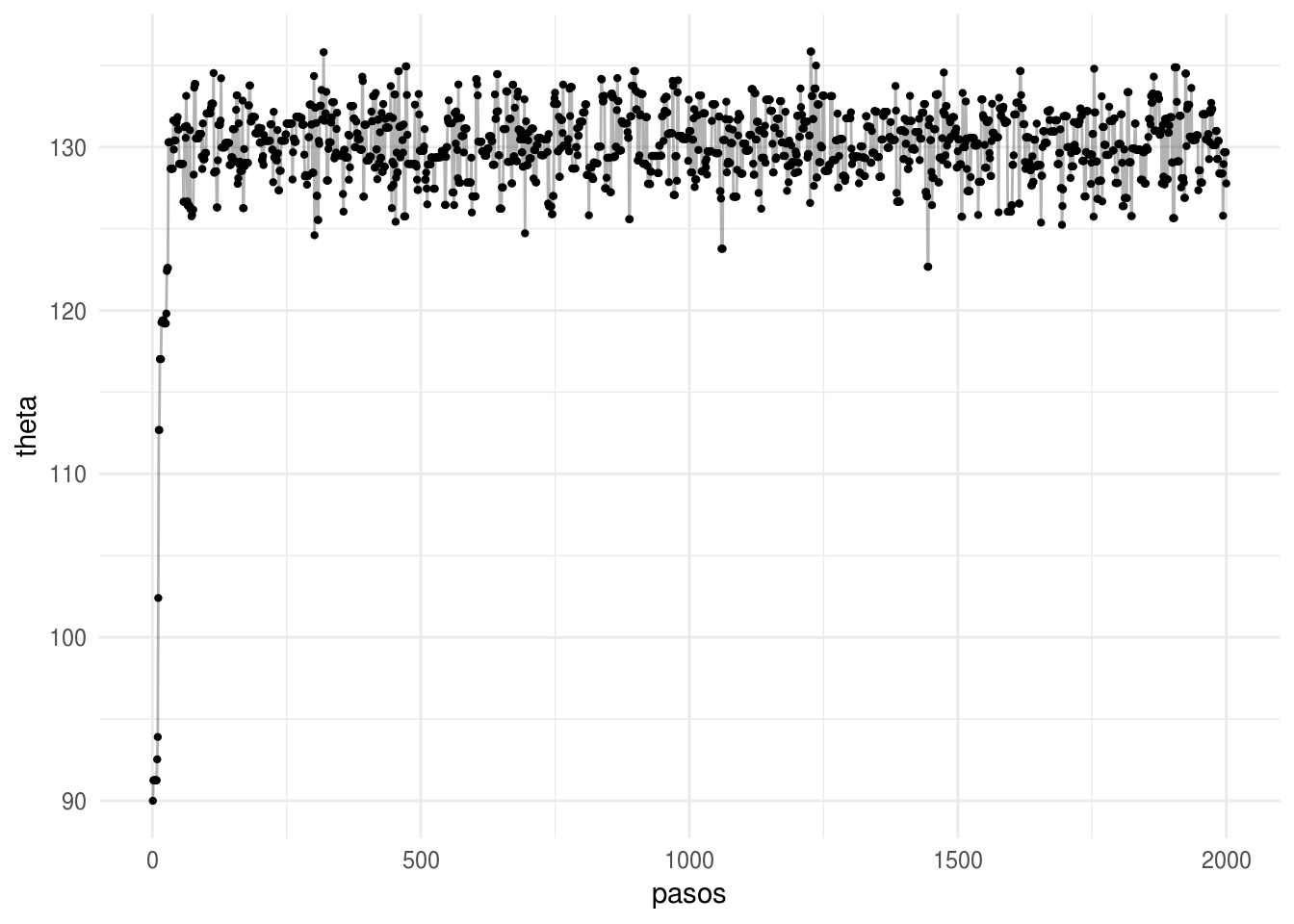
ggplot(filter(caminata, pasos > 2000), aes(x = theta)) +
geom_histogram(aes(y = ..density..), binwidth = 0.8) 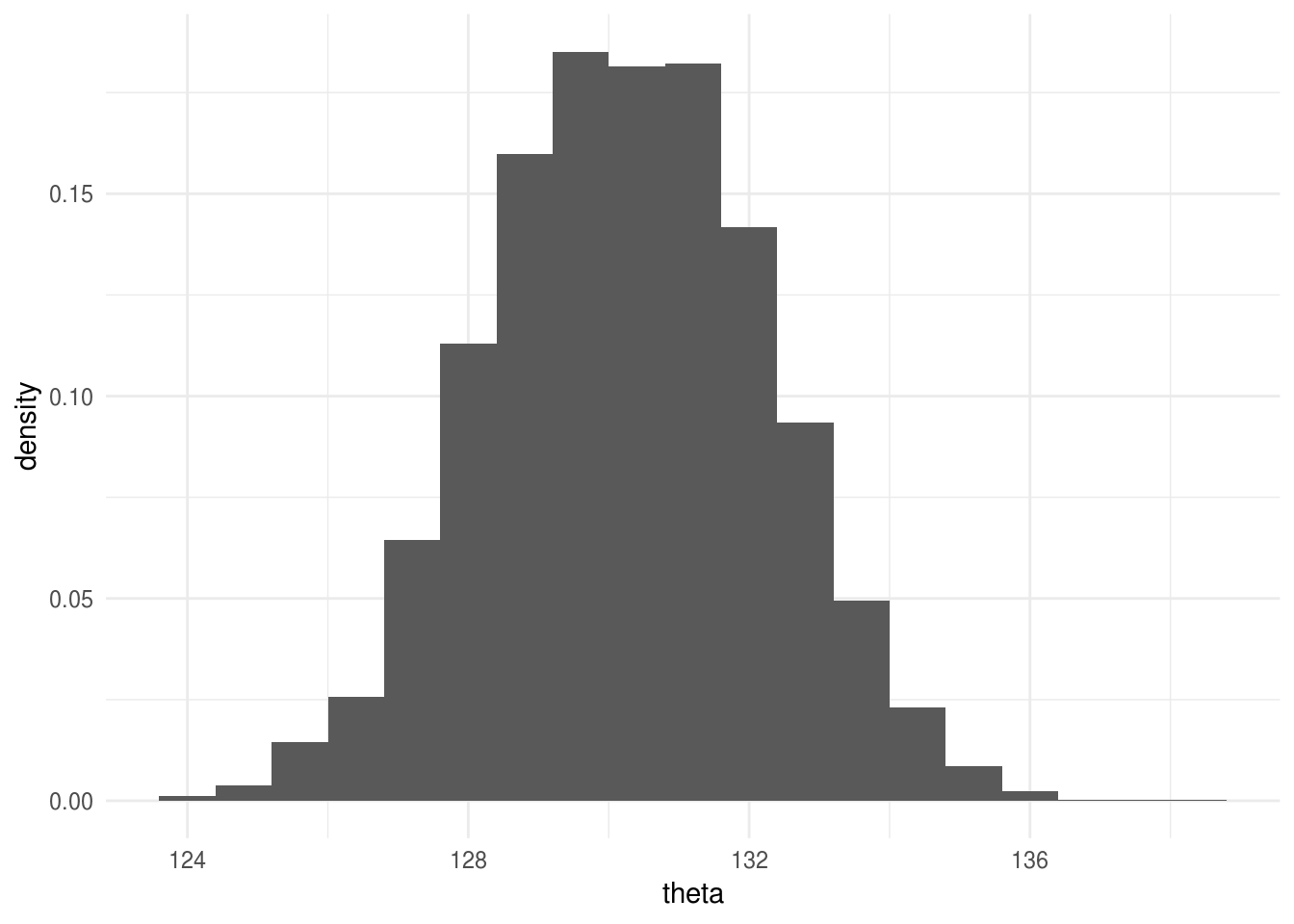
ggplot(filter(caminata, pasos > 2000), aes(x = theta)) +
geom_histogram(aes(y = ..density..), binwidth = 0.7) +
stat_function(fun = dnorm, args = list(mean = 130.3, sd = 1.98), color = "red")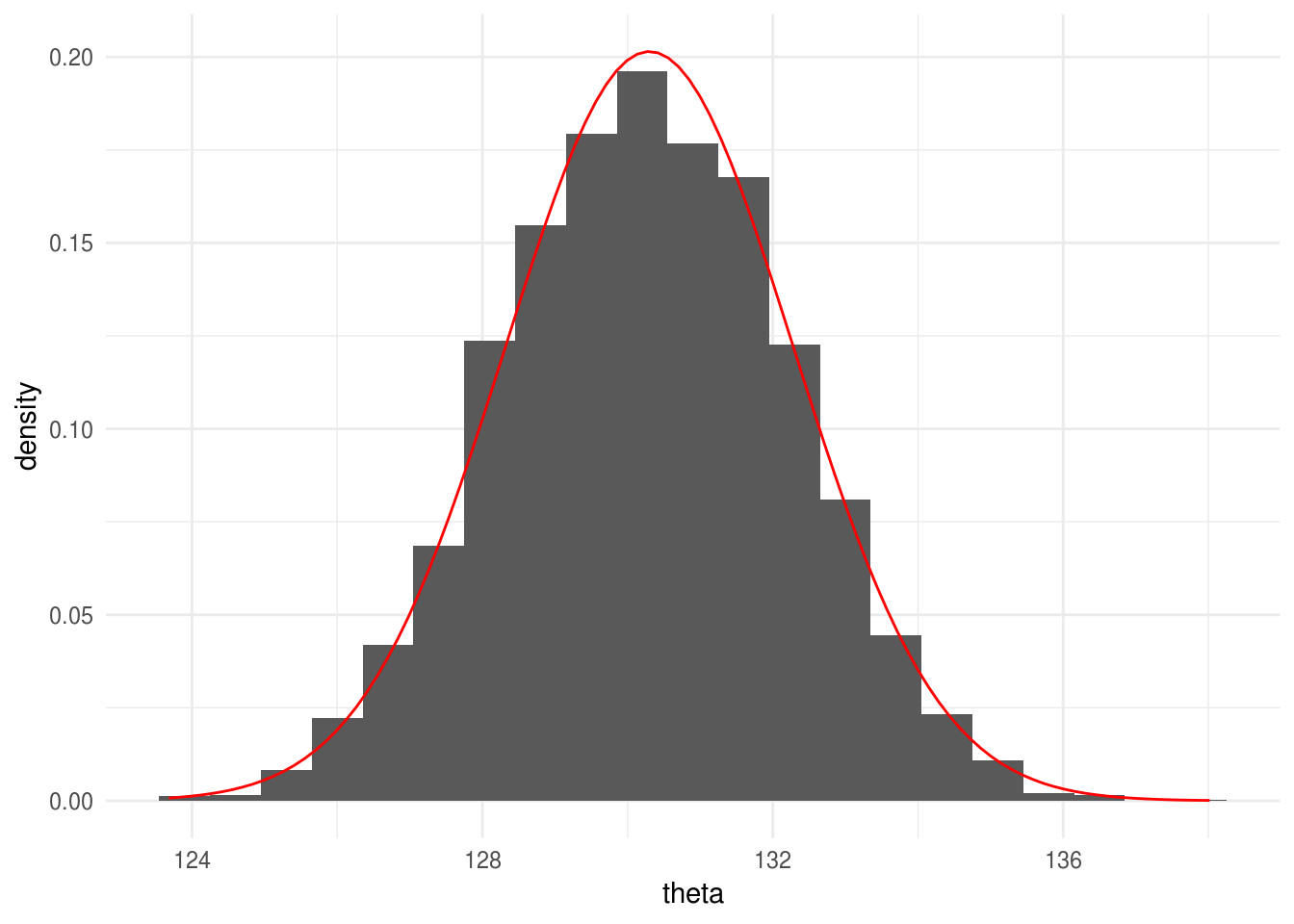
sigma ^ 2 * mu / (sigma ^ 2 + N * tau ^ 2) + tau ^ 2 * S / (sigma^2 + N * tau^2) # media
#> [1] 130
sigma ^ 2 * tau ^ 2 / (sigma ^ 2 + N * tau ^ 2)
#> [1] 3.93- Elegir varianza grande nos daría una inicial poco informativa.