9-Inferencia gráfica, tamaño de muestra, bootstrap paramétrico.
Inferencia gráfica
Los datos marg_diabetes incluyen información de marginación y diabetes en México:
ent,id_ent,mun,id_mun,cvegeo: corresponden al estado, municipio y sus códigos de identificación.n_causaes el número de muertes de adultos mayores a \(65\) años a causa de diabetes en \(2015\), ytasa_munla tasa correspondiente por cada \(10,000\) habitantes.tasa_alf(porcentaje de población alfabeta),ind_des_hum(índice de desarrollo humano),conapo(índice de marginación).
Utiliza los datos para explorar gráficamente la relación entre algunas de las variables, utiliza el protocolo lineup para hacer inferencia gráfica.
Simulación para calcular tamaños de muestra
Supongamos que queremos hacer una encuesta para estimar la proporción de hogares donde se consume refresco de manera regular, para ello se diseña un muestreo por conglomerados donde los conglomerados están dados por conjuntos de hoagres de tal manera que todos los conglomerados tienen el mismo número de hogares. La selección de la muestra se hará en dos etapas:
Seleccionamos \(J\) conglomerados de manera aleatoria.
En cada conglomerado seleccionames \(n/J\) hogares para entrevistar.
El estimador será simplemente el porcentaje de hogares del total de la muestra. Suponemos que la verdadera proporción es cercana a \(0.50\) y que la media de la proporción de interés a lo largo de los conglomerados tiene una desviación estándar de \(0.1\).
Supongamos que la muestra total es de \(n=1000\). ¿Cuál es la estimación del error estándar para la proporción estimada si \(J=1,10,100,1000\)?
El obejtivo es estimar la propoción que consume refresco en la población con un error estándar de a lo más \(2\%\). ¿Que valores de \(J\) y \(n\) debemos elegir para cumplir el objetivo al menor costo?
Los costos del levantamiento son: + \(50\) pesos por encuesta. + \(500\) pesos por conglomerado
Bootstrap paramétrico
- Sean \(X_1,...,X_n \sim N(\mu, 1)\). Sea \(\theta = e^{\mu}\), crea una base de datos usando \(\mu=5\) que consista de \(n=100\) observaciones.
Usa el método delta para estimar \(\hat{se}\) y crea un intervalo del \(95\%\) de confianza. Usa boostrap paramétrico para crear un intervalo del \(95\%\). Usa bootstrap no paramétrico para crear un intervalo del \(95\%\). Compara tus respuestas.
Realiza un histograma de replicaciones bootstrap para cada método, estas son estimaciones de la distribución de \(\hat{\theta}\). El método delta también nos da una aproximación a esta distribución: \(Normal(\hat{\theta},\hat{se}^2)\). Comparalos con la verdadera distribución de \(\hat{\theta}\) (que puedes obtener vía simulación). ¿Cuál es la aproximación más cercana a la verdadera distribución?
Pista: \(se(\hat{\mu}) = 1/\sqrt{n}\)
Solución
Simulación para calcular tamaños de muestra
muestreo <- function(J, n_total = 1000) {
n_cong <- floor(n_total / J)
medias <- rnorm(J, 0.5, 0.1)
medias <- ifelse(medias < 0, 0,
ifelse(medias > 1, 1, medias))
resp <- rbinom(J, n_cong, medias)
sum(resp) / n_total
}
errores <- data_frame(J = c(1, 10, 100, 1000)) %>%
mutate(
sims = map(J, ~(rerun(1000, muestreo(.)) %>% flatten_dbl())),
error_est = map_dbl(sims, sd) %>% round(3)
)
errores
#> # A tibble: 4 x 3
#> J sims error_est
#> <dbl> <list> <dbl>
#> 1 1 <dbl [1,000]> 0.102
#> 2 10 <dbl [1,000]> 0.036
#> 3 100 <dbl [1,000]> 0.018
#> 4 1000 <dbl [1,000]> 0.015
tamano_muestra <- function(J) {
n_total <- max(100, J)
ee <- rerun(1000, muestreo(J = J, n_total = n_total)) %>%
flatten_dbl() %>% sd()
while(ee > 0.02){
n_total = n_total + 20
ee <- rerun(500, muestreo(J = J, n_total = n_total)) %>%
flatten_dbl() %>% sd() %>% round(3)
}
list(ee = ee, n_total = n_total, costo = 500 * J + 50 * n_total)
}
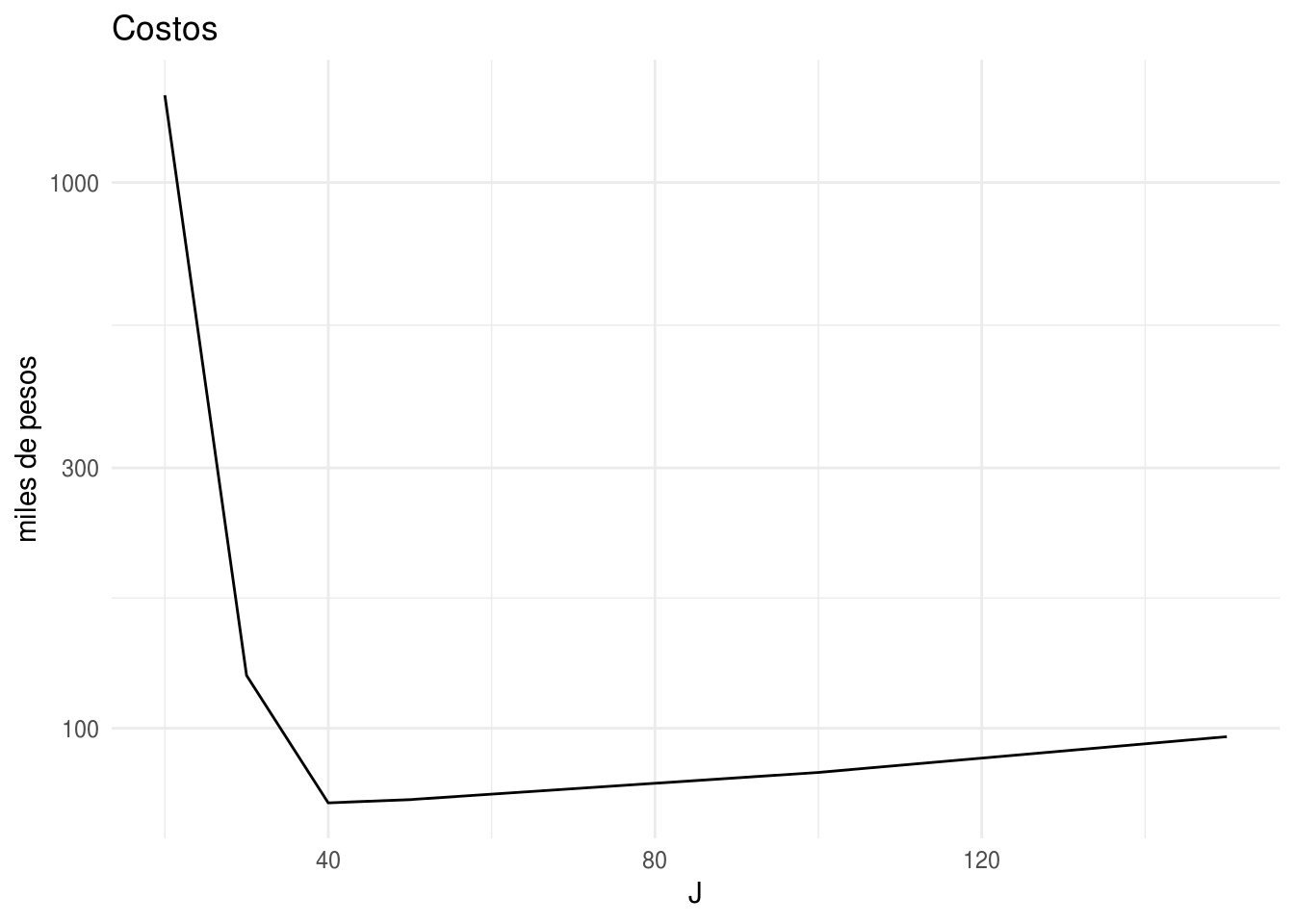
tamanos <- c(20, 30, 40, 50, 100, 150)
costos <- map_df(tamanos, tamano_muestra)
costos$J <- tamanos
costos
#> # A tibble: 6 x 4
#> ee n_total costo J
#> <dbl> <dbl> <dbl> <dbl>
#> 1 0.02 28700 1445000 20
#> 2 0.02 2200 125000 30
#> 3 0.019 1060 73000 40
#> 4 0.02 980 74000 50
#> 5 0.019 660 83000 100
#> 6 0.019 430 96500 150
ggplot(costos, aes(x = J, y = costo / 1000)) +
geom_line() + scale_y_log10() + theme_minimal() +
labs(y = "miles de pesos", title = "Costos")