10.2 Regla de Bayes e inferencia bayesiana
Thomas Bayes (\(1702-1761\)) fue un matemático y ministro de la iglesia presbiteriana, en \(1764\) se publicó su famoso teorema.
Una aplicación crucial de la regla de Bayes es determinar la probabilidad de un modelo dado un conjunto de datos. Lo que el modelo determina es la probabilidad de los datos condicional a valores particulares de los parámetros y a la estructura del modelo. Por su parte usamos la regla de Bayes para ir de la probabilidad de los datos, dado el modelo, a la probabilidad del modelo, dados los datos.
Ejemplo: Lanzamientos de monedas
Comencemos recordando la regla de Bayes usando dos variables aleatorias discretas. Lanzamos una moneda \(3\) veces, sea \(X\) la variable aleatoria correspondiente al número de Águilas observadas y \(Y\) registra el número de cambios entre águilas y soles.
Escribe la distribución conjunta de las variables, y las distribuciones marginales.
Considera la probabilidad de observar un cambio condicional a que observamos un águila y compara con la probabilidad de observar un águila condicional a que observamos un cambio.
Para entender probabilidad condicional podemos pensar en restringir nuestra atención a una única fila o columna de la tabla. Supongamos que alguien lanza una moneda \(3\) veces y nos informa que la secuencia contiene exactamente un cambio. Dada esta información podemos restringir nuestra atención a la fila correspondiente a un solo cambio. Sabemos que ocurrió uno de los eventos de esa fila. Las probabilidades relativas de los eventos de esa fila no han cambiado pero sabemos que la probabilidad total debe sumar uno, por lo que simplemente normalizamos dividiendo entre \(p(C=1)\). En este ejemplo vemos que cuando no sabemos nada acerca del número de cambios, todo lo que sabemos de número de águilas está contenido en la distribución marginal de \(X\), por otro lado, si sabemos que hubo un cambio entonces sabemos que estamos en los escenarios de la fila correspondiente a un cambio, y calculamos estas probabilidades condicionales. Es así que nos movemos de creencias iniciales (marginal) acerca de \(X\) a creecnias posteriores (condicional).
Regla de Bayes en modelos y datos
Una de las aplicaciones más importantes de la regla de Bayes es cuando las variables fila y columna son datos y parámetros del modelo respectivamente.
Un modelo especifica la probabilidad de valores particulares dado la estructura del modelo y valores de los parámetros. Por ejemplo en un modelo de lanzamientos de monedas tenemos \[p(x = A|\theta)=\theta\],
\[p(x = S|\theta)= 1- \theta\]
De manera general, el modelo especifica:
\[p(\text{datos}|\text{valores de parámetros y estructura del modelo})\]
y usamos la regla de Bayes para convertir la expresión anterior a lo que nos interesa de verdad, que es, que tanta certidumbre tenemos del modelo condicional a los datos:
\[p(\text{valores de parámetros y estructura del modelo} | \text{datos})\]
Una vez que observamos los datos, usamos la regla de Bayes para determinar o actualizar nuestras creencias de posibles parámetros y modelos.
Entonces:
Cuantificamos la información (o incertidumbre) acerca del parámetro desconocido \(\theta\) mediante distribuciones de probabilidad.
Antes de observar datos \(x\), cuantificamos la información de \(\theta\) externa a \(x\) en una distribución a priori:
\[p(\theta),\] esto es, la distribución a priori resume nuestras creencias acerca del parámetro ajenas a los datos. Por otra parte, cuantificamos la información de \(\theta\) asociada a \(x\) mediante la distribución de verosimilitud
\[p(x|\theta)\]
- Combinamos la información a priori y la información que provee \(x\) mediante el teorema de Bayes obteniendo así la distribución posterior
\[p(\theta|x) \propto p(x|\theta)p(\theta).\]
- Las inferencias se obtienen de resúmenes de la distribución posterior.
Ejemplo: Ingesta calórica en estudiantes
Supongamos que nos interesa aprender los hábitos alimenticios de los estudiantes universitarios en México, y escuchamos que de acuerdo a investigaciones se recomienda que un adulto promedio ingiera \(2500\) kcal. Es así que buscamos conocer que proporción de los estudiantes siguen esta recomendación, para ello tomaremos una muestra aleatoria de estudiantes del ITAM. Denotemos por \(\theta\) la proporción de estudiantes que ingieren en un día \(2500\) kcal o más. El valor de \(\theta\) es desconocido, y desde el punto de vista bayesiano cuando tenemos incertidumbre de algo (puede ser un parámetro o una predicción) lo vemos como una variable aleatoria y por tanto tiene asociada una distribución de probabilidad que actualizaremos conforme obtenemos información (observamos datos).
Recordemos que la distribución \(p(\theta)\) se conoce como la distribución a priori y representa nuestras creencias de los posibles valores que puede tomar el parámetro. Supongamos que tras leer artículos y entrevistar especialistas consideramos los posibles valores de \(\theta\) y les asigmanos pesos:
library(tidyverse)
theta <- seq(0.05, 0.95, 0.1)
pesos.prior <- c(1, 5.2, 8, 7.2, 4.6, 2.1, 0.7, 0.1, 0, 0)
prior <- pesos.prior/sum(pesos.prior)
prior_df <- data_frame(theta, prior = round(prior, 3))
prior_df
#> # A tibble: 10 x 2
#> theta prior
#> <dbl> <dbl>
#> 1 0.05 0.035
#> 2 0.15 0.18
#> 3 0.25 0.277
#> 4 0.35 0.249
#> 5 0.45 0.159
#> 6 0.55 0.073
#> 7 0.65 0.024
#> 8 0.75 0.003
#> 9 0.85 0
#> 10 0.95 0Una vez que cuantificamos nuestro conocimiento (o la falta de este) sobre los posibles valores que puede tomar \(\theta\) especificamos la verosimilitud y la distribución conjunta \(p(x, \theta)\), donde \(x = (x_1,...,x_N)\) veamos la distribución de un estudiante en particular: \[p(x_i|\theta) \sim Bernoulli(\theta),\] para \(i=1,...,N\), es decir, condicional a \(\theta\) la probabilidad de que un estudiante ingiera más de \(2500\) calorías es \(\theta\) y la función de verosimilitud \(p(x_1,...,x_N|\theta) = \mathcal{L}(\theta)\):
\[p(x_1,...,x_N|\theta) = \prod_{n=1}^N p(x_n|\theta)\] \[= \theta^z(1 - \theta)^{N-z}\]
donde \(z\) denota el número de estudiantes que ingirió al menos \(2500\) kcal y \(N-z\) el número de estudiantes que ingirió menos de \(2500\) kcal.
Ahora calculamos la distribución posterior de \(\theta\) usando la regla de Bayes:
\[p(\theta|x) = \frac{p(x_1,...,x_N,\theta)}{p(x)}\] \[\propto p(\theta)\mathcal{L}(\theta)\]
Vemos que la distribución posterior es proporcional al producto de la verosimilitud y la distribución inicial, el denominador \(p(x)\) no depende de \(\theta\) por lo que es constante (como función de \(\theta\)) y esta ahí para normalizar la distribución posterior asegurando que tengamos una distribución de probabilidad.
Inicial discreta
Volviendo a nuestro ejemplo, usamos la inicial discreta que discutimos (tabla de pesos normalizados) y supongamos que tomamos una muestra de \(30\) alumnos de los cuales \(z=11\) ingieren al menos \(2500\) kcal, calculemos la distribución posterior de \(\theta\), usando que
\[\mathcal{L}(\theta) = \theta^{z}(1-\theta)^{N-z}\] con \(0<\theta<1\)
library(LearnBayes)
N <- 30 # estudiantes
z <- 11 # éxitos
# Verosimilitud
Like <- theta ^ z * (1 - theta) ^ (N - z)
product <- Like * prior
# Distribución posterior (normalizamos)
post <- product / sum(product)
dists <- bind_cols(prior_df, post = post)
round(dists, 3)
#> # A tibble: 10 x 3
#> theta prior post
#> <dbl> <dbl> <dbl>
#> 1 0.05 0.035 0
#> 2 0.15 0.18 0.006
#> 3 0.25 0.277 0.22
#> 4 0.35 0.249 0.529
#> 5 0.45 0.159 0.224
#> 6 0.55 0.073 0.021
#> 7 0.65 0.024 0
#> 8 0.75 0.003 0
#> 9 0.85 0 0
#> 10 0.95 0 0
# También podemos usar la función pdisc
pdisc(p = theta, prior = prior, data = c(z, N - z)) %>% round(3)
#> [1] 0.000 0.006 0.220 0.529 0.224 0.021 0.000 0.000 0.000 0.000
# Alargamos los datos para graficar
dists_l <- dists %>%
gather(dist, val, prior:post) %>%
mutate(dist = factor(dist, levels = c("prior", "post")))
ggplot(dists_l, aes(x = theta, y = val)) +
geom_bar(stat = "identity", fill = "darkgray") +
facet_wrap(~ dist) +
labs(x = expression(theta), y = expression(p(theta))) 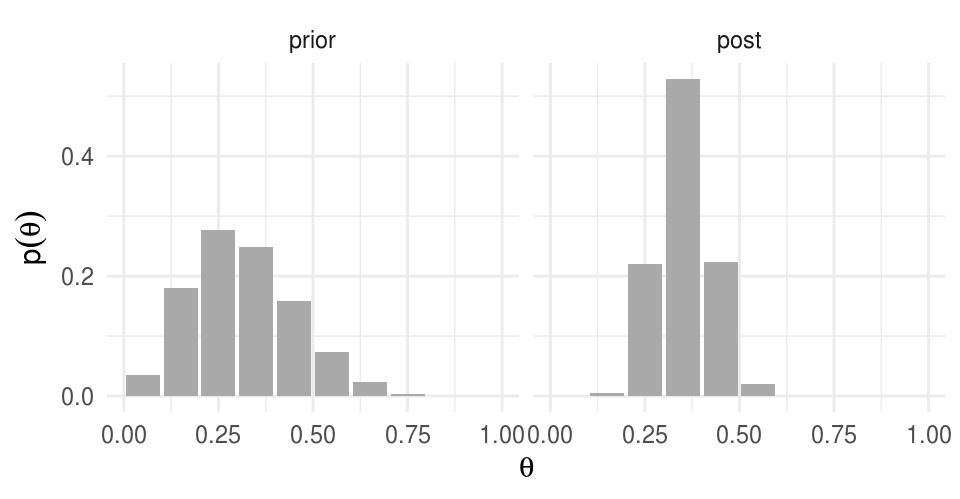
 ¿Cómo se ve la distribución posterior si tomamos
una muestra de tamaño \(90\) donde observamos la misma proporción de éxitos.
Realiza los cálculos y graficala como un panel adicional de la gráfica
anterior.
¿Cómo se ve la distribución posterior si tomamos
una muestra de tamaño \(90\) donde observamos la misma proporción de éxitos.
Realiza los cálculos y graficala como un panel adicional de la gráfica
anterior.
- ¿Cómo definirías la distribución inicial si no tuvieras conocimiento de los artículos y expertos?
Evidencia
Ahora, en el teorema de Bayes también encontramos el término \(p(x)\) que denominamos la evidencia, también se conoce como verosimilitud marginal o inicial predictiva. \[p(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)}\]
La evidencia es la probabilidad de los datos de acuerdo al modelo y se calcula sumando a lo largo de todos los posibles valores de los parámetros y ponderando por nuestra certidumbre en esos valores de los parámetros.
Es importante notar que hablamos de valores de los parámetros \(\theta\) únicamente en el contexto de un modelo particular pues este el que da sentido a los parámetros. Podemos hacer evidente el modelo en la notación,
\[p(\theta|x,M)=\frac{p(x|\theta,M)p(\theta|M)}{p(x|M)}\]
en este contexto la evidencia se define como:
\[p(x|M)=\int p(x|\theta,M)p(\theta|M)d\theta\]
La notación anterior es conveniente sobre todo cuando estamos considerando más de un modelo y queremos usar los datos para determinar la certeza que tenemos en cada modelo. Supongamos que tenemos dos modelos \(M_1\) y \(M_2\), entonces podemos calcular el cociente de \(p(M_1|x)\) y \(p(M_2|x)\) obteniendo:
\[\frac{p(M_1|x)}{p(M_2|x)} = \frac{p(x|M_1) \cdot p(M_1)}{p(x|M_2)\cdot p(M_2)}\]
El cociente de evidencia \(\frac{p(x|M_1)}{p(x|M_2)}\) se conoce como factor de Bayes, y \(p(M_i)\) describe nuestras creencias iniciales en cada modelo.
Invarianza en el orden de los datos
Vimos que la regla de Bayes nos permite pasar del conocimiento inicial \(p(\theta)\) al posterior \(p(\theta|x)\) conforme recopilamos datos. Supongamos ahora que observamos más datos, los denotamos \(x'\), podemos volver a actualizar nuestras creencias pasando de \(p(\theta|x)\) a \(p(\theta|x,x')\). Entonces podemos preguntarnos si nuestro conocimiento posterior cambia si actualizamos de acuerdo a \(x\) primero y después \(x'\) o vice-versa. La respuesta es que si \(p(x|\theta)\) y \(p(x'|\theta)\) son iid entonces el orden en que actualizamos nuestro conocimiento no afecta la distribución posterior.
La invarianza al orden tiene sentido intuitivamente: Si la función de verosimilitud no depende del tiempo o del ordenamineto de los datos, entonces la posterior tampoco tiene porque depender del ordenamiento de los datos.
Like <- theta ^ 1 * (1 - theta) ^ (1 - 1)
product <- Like * prior$p
post <- product / sum(product)
post
#> [1] 0.125 0.500 0.375Objetivos de la inferencia
Los tres objetivos de la inferencia son: estimación de parámetros, predicción de valores y comparación de modelos.
- La estimación de parámetros implica determinar hasta que punto creemos en
cada posible valor del parámetro. En estadística bayesiana la estimación se
realiza con la distribución posterior sobre los valores
de los parámetros \(\theta\).
La siguiente gráfica ejemplifica un experimento Bernoulli, con dos posibles iniciales, los datos observados son \(N=20\) lanzamientos de moneda que resultan en \(12\) éxitos o águilas.
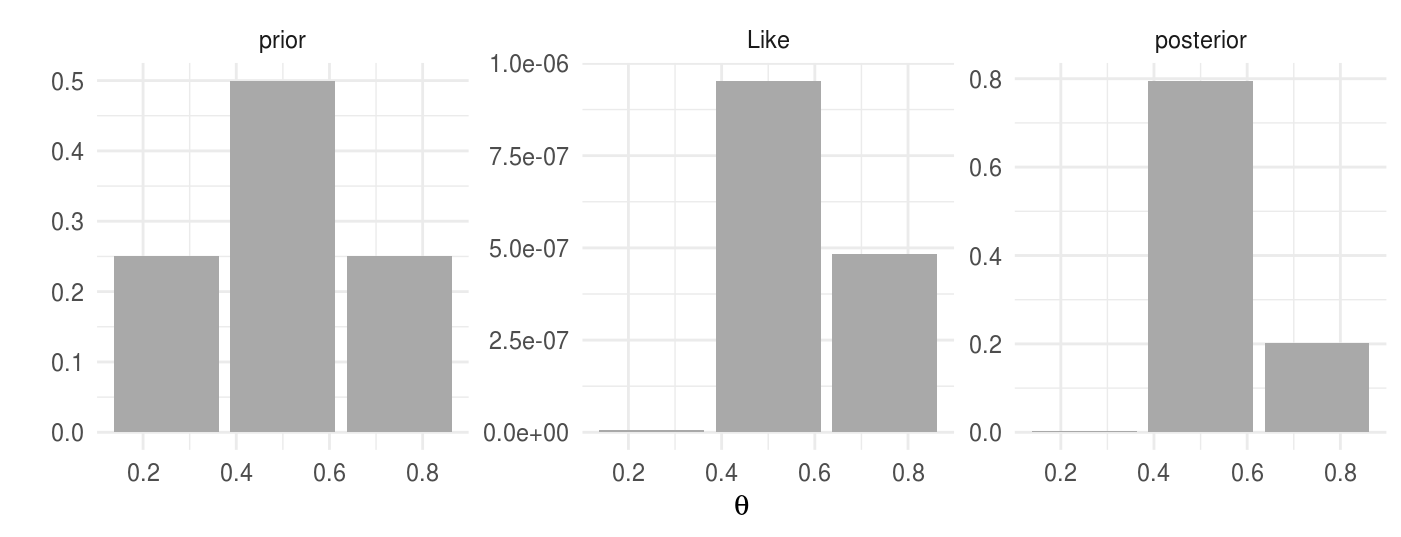
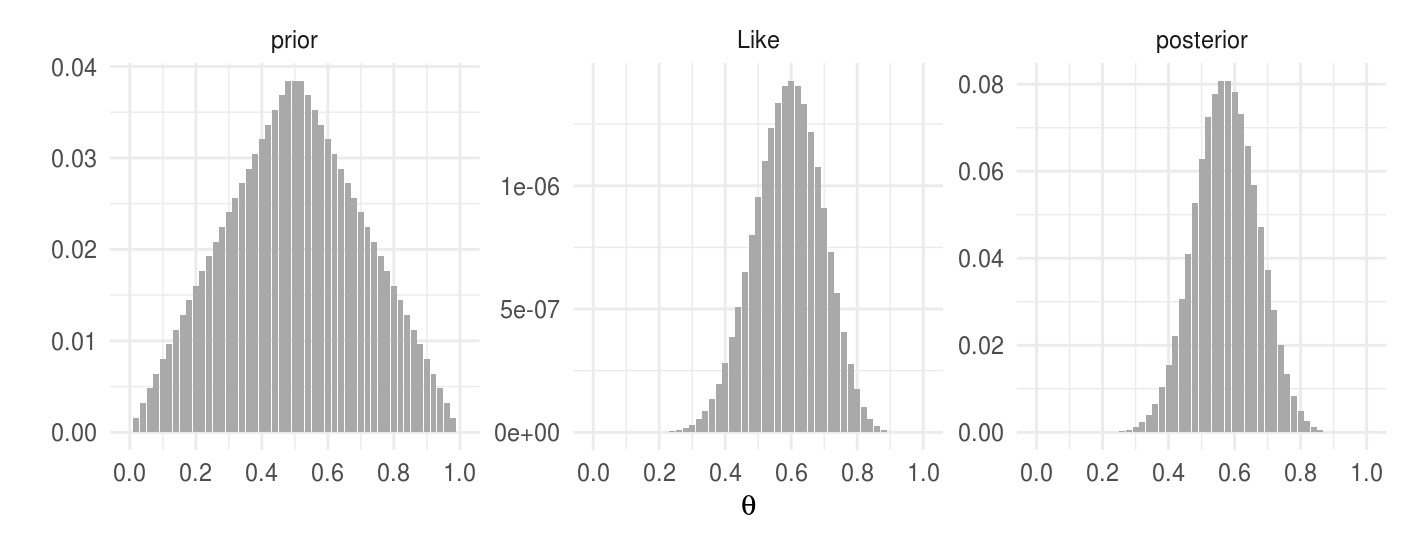
- Predicción de valores. Usando nuestro conocimiento actual nos interesa
predecir la probabilidad de datos futuros. La probabilidad predictiva de un
dato \(y\) (no observado) se determina promediando las probabilidades predictivas
de los datos a lo largo de todos los posibles valores de los parámetros y
ponderados por la creencia en los valores de los parámetros. Cuando solo
contamos con nuestro conocimiento incial tendríamos:
\[p(y) =\int p(y|\theta)p(\theta)d\theta\]
Notese que la ecuación anterior coincide con la correspondiente a la evidencia,
con la diferencia de que la evidencia se refiere a un valor observado y en
esta ecuación estamos calculando la probabilidad de cualquier valor \(y\).
Una vez que obserbamos datos tenemos la distribución predictiva posterior: \[p(y|x) =\int p(y|\theta)p(\theta|x)d\theta\] Por ejemplo podemos usar las creencias iniciales del modelo \(1\), que propusimos arriba para calcular la probabilidad predictiva de observar águila:
\[p(y=S) = \sum_{\theta}p(y=A|\theta)p(\theta) = 0.5\]
Vale la pena destacar que las prediciones son probabilidades de cada posible valor condicional a nuestro modelo de creencias actuales. Si nos interesa predecir un valor particular en lugar de una distribución a lo largo de todos los posibles valores podemos usar la media de la distribución predictiva. Por tanto el valor a predecir sería:
\[p(y)=\int y p(y) dy\]
La integral anterior únicamente tiene sentido si \(y\) es una variable continua. Si \(y\) es nominal, como el resultado de un volado, entonces podemos usar el valor más probable.
- Comparación de modelos, una caracterítica conveniente de la comparación de modelos en estadística bayesiana es que la complejidad del modelo se toma en cuenta de manera automática.
Recordemos los dos modelos discretos, en el primero supusimos que el parámetro \(\theta\) únicamente puede tomar uno de \(3\) valores \((0.25, 0.5, 0.75)\), esta restricción dió lugar a un modelo simple. Por su parte, el modelo \(2\) es más complejo y permite muchos más valores de \(\theta\) (\(51\)). La forma de la distribución inicial es triangular en ambos casos y el valor de mayor probabilidad inicial es \(\theta = 0.50\) y reflejamos que creemos que es menos factible que el valor se encuentre en los extremos.
Podemos calcular el factor de Bayes para distintos datos observados:
# Modelo 1, 3 posibles valores
p_M1 <- data_frame(theta = c(0.25, 0.5, 0.75), prior = c(0.25, 0.5, 0.25),
modelo ="M1")
# Modelo 2, Creamos una inicial que puede tomar más valores
p <- seq(0, 24, 1)
p2 <- c(p, 24, sort(p, decreasing = TRUE))
p_M2 <- data_frame(theta = seq(0, 1, 0.02), prior = p2 / sum(p2),
modelo = "M2")
N <- 20 # estudiantes
z <- 12 # éxitos
dists_h <- bind_rows(p_M1, p_M2) %>% # base de datos horizontal
group_by(modelo) %>%
mutate(
Like = theta ^ z * (1 - theta) ^ (N - z), # verosimilitud
posterior = (Like * prior) / sum(Like * prior)
)
dists <- dists_h %>% # base de datos larga
gather(dist, valor, prior, Like, posterior) %>%
mutate(dist = factor(dist, levels = c("prior", "Like", "posterior")))
factorBayes <- function(N, z){
evidencia <- bind_rows(p_M1, p_M2) %>% # base de datos horizontal
group_by(modelo) %>%
mutate(
Like = theta ^ z * (1 - theta) ^ (N - z), # verosimilitud
posterior = (Like * prior) / sum(Like * prior)
) %>%
summarise(evidencia = sum(prior * Like))
print(evidencia)
return(evidencia[1, 2] / evidencia[2, 2])
}
factorBayes(50, 25)
#> # A tibble: 2 x 2
#> modelo evidencia
#> <chr> <dbl>
#> 1 M1 4.44e-16
#> 2 M2 2.75e-16
#> evidencia
#> 1 1.61
factorBayes(100, 75)
#> # A tibble: 2 x 2
#> modelo evidencia
#> <chr> <dbl>
#> 1 M1 9.46e-26
#> 2 M2 4.17e-26
#> evidencia
#> 1 2.27
factorBayes(100, 10)
#> # A tibble: 2 x 2
#> modelo evidencia
#> <chr> <dbl>
#> 1 M1 1.36e-18
#> 2 M2 2.47e-16
#> evidencia
#> 1 0.00549
factorBayes(40, 38)
#> # A tibble: 2 x 2
#> modelo evidencia
#> <chr> <dbl>
#> 1 M1 0.000000279
#> 2 M2 0.00000895
#> evidencia
#> 1 0.0312¿Cómo explicarías los resultados anteriores?
La evidencia de un modelo \(p(x|M)\) no dice mucho por si misma, si no que es mas relevante en el contexto del factor de Bayes (la evidencia relativa de dos modelos). Es importante recordar que la comparación de modelos nos habla únicamente de la evidencia relativa de un modelo; sin embargo, puede que ninguno de los modelos que estamos considerando sean adecuados para nuestros datos, por lo que más adelante estudiaremos maneras de evaluar un modelo.
Cálculo de la distribución posterior
En la inferencia Bayesiana se requiere calcular el denominador de la fórmula de Bayes \(p(x)\), es común que esto requiera que se calcule una integral complicada; sin embargo, hay algunas maneras de evitar esto,
El camino tradicional consiste en usar funciones de verosimilitud con dsitribuciones iniciales conjugadas. Cuando una distribución inicial es conjugada de la verosimilitud resulta en una distribución posterior con la misma forma funcional que la distribución inicial.
Otra alternativa es aproximar la integral numericamente. Cuando el espacio de parámetros es de dimensión chica, se puede cubrir con una cuadrícula de puntos y la integral se puede calcular sumando a través de dicha cuadrícula. Sin embargo cuando el espacio de parámetros aumenta de dimensión el número de puntos necesarios para la aproximación crece demasiado y hay que recurrir a otas técnicas.
Se ha desarrollado una clase de métodos de simulación para poder calcular la distribución posterior, estos se conocen como cadenas de Markov via Monte Carlo (MCMC por sus siglas en inglés). El desarrollo de los métodos MCMC es lo que ha propiciado el desarrollo de la estadística bayesiana en años recientes.