5.2 Interpretación frecuentista de probabilidad
La interpretación de la probabilidad como extensión a la idea de proporción es fundamental, pero deja sin responder una pregunta crítica:
- ¿Cómo sabemos que un modelo probabilístico de este tipo describe apropiadamente la realidad? ¿Qué pruebas empíricas podemos buscar que de soporte a tal modelo?
El concepto subyacente que tardó más en formalizarse es el siguiente. En términos de juegos justos:
- A partir de una sola repetición del juego, no podemos determinar si un juego es justo o no.
- Sin embargo, si repetimos una gran cantidad de veces el juego justo, nuestras pérdidas y ganancias deberían equilibrarse, y con seguridad nuestro balance será cercano a 0.
Ejemplo
Según el concepto de juego justo, si mi probabilidad de ganar es \(p\), es justo que apueste una cantidad \(Ap\) y mi contrincante una cantidad \(A(1-p)\). Después de \(n\) repeticiones de este juego, supongamos que gané un número de veces \(m\). Entonces, tengo \(A(1-p)m\) pesos de las veces que gané, y perdí \(Ap(n-m)\) pesos por las veces que perdí. En total, mi neto de ganancias es \(A(1-p)m - Ap(n-m)\). Si esta cantidad es cercana a cero \[A(1-p)m - Ap(n-m) \approx 0,\] entonces despejando obtenemos que \[p \approx \frac{m}{n},\] Es decir, aproximadamente tengo que ganar una fracción \(m/n\) de veces. Esta cantidad es una frecuencia relativa de ocurrencia.
Una frecuencia relativa es una proporción que mide que tan seguido, o frecuente, ocurre una u otra cosa en una sucesión de observaciones. Pensemos en un experimento que se pueda repetir, por ejemplo, lanzar una moneda, lanzar un dado, el nacimiento de un bebé. Llamaremos ensayo a una repetición del experimento. Ahora, sea A un posible resultado del evento (obtener sol, obtener un 6, el bebé es niña), si A ocurre \(m\) veces en \(n\) ensayos, entonces la frecuencia relativa de A en \(n\) ensayos es \(m/n\).
Ejemplo
Supongamos que lanzamos una moneda 10 veces y obtenemos los siguientes resultados:
set.seed(2881)
lanzamientos_10 <- sample(c("A", "S"), 10, replace = TRUE)
lanzamientos_10
#> [1] "A" "A" "A" "A" "A" "A" "S" "A" "A" "A"Podemos calcular las secuencia de frecuencias relativas de águila:
Resultados empíricos acerca de frecuencias relativas
Una primera observación empírica es que las frecuencias relativas basadas en un número mayor de observaciones son menos fluctuantes comparado con las frecuencias relativas basadas en pocas observaciones.
Este fenómeno se conoce a veces como la ley empírica de los promedios (que se formaliza después en las leyes de los grandes números):
n <- 1000
tibble(num_lanzamiento = 1:n, lanzamiento = sample(c("A", "S"), n,
replace = TRUE)) %>%
mutate(frec_rel = cummean(lanzamiento == "A")) %>%
ggplot(aes(x = num_lanzamiento, y = frec_rel)) +
geom_hline(yintercept = 0.5, color = "red", alpha = 0.5) +
geom_line(color = "darkgray") +
geom_point(size = 1.0) +
labs(y = "frecuencia relativa", title = "1000 volados",
x = "lanzamiento")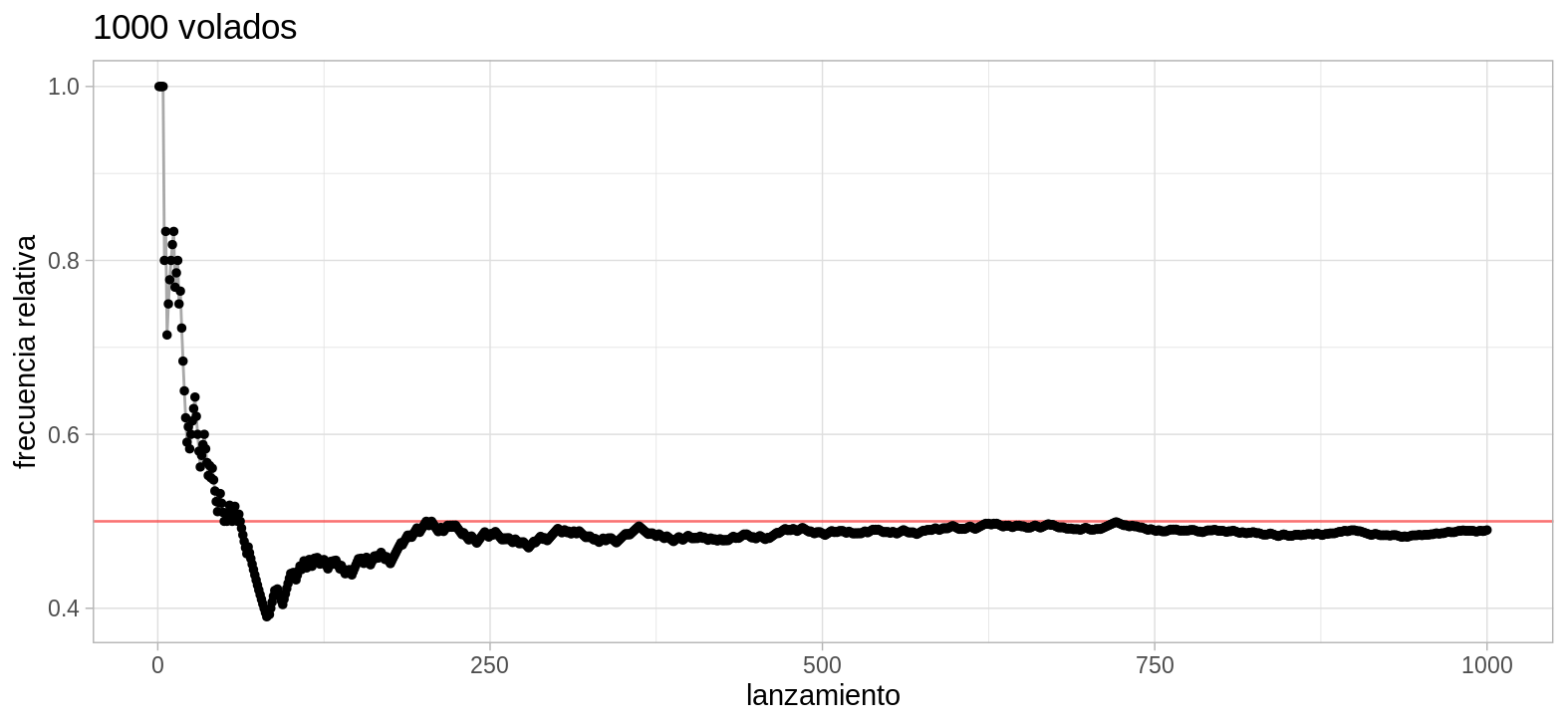
Veamos las frecuencias relativas para 3 series de 1000 lanzamientos.
lanzar <- function(n = 1000){
tibble(num_lanzamiento = 1:n, lanzamiento = sample(c("A", "S"), n,
replace = TRUE)) %>%
mutate(frec_rel = cummean(lanzamiento == "A"))
}
head(lanzar())
#> # A tibble: 6 x 3
#> num_lanzamiento lanzamiento frec_rel
#> <int> <chr> <dbl>
#> 1 1 A 1
#> 2 2 S 0.5
#> 3 3 A 0.667
#> 4 4 S 0.5
#> 5 5 S 0.4
#> 6 6 S 0.333
set.seed(31287931)
# usamos la función map_df del paquete purrr
map_df(1:3, ~lanzar(), .id = "serie") %>%
ggplot(aes(x = log(num_lanzamiento), y = frec_rel,
color = as.character(serie))) +
geom_hline(yintercept = 0.5, color = "darkgray") +
geom_line() +
scale_x_continuous("lanzamiento", labels = exp,
breaks = log(sapply(0:10, function(i) 2 ^ i))) +
labs(color = "serie", y = "frecuencia relativa", title = "1000 volados")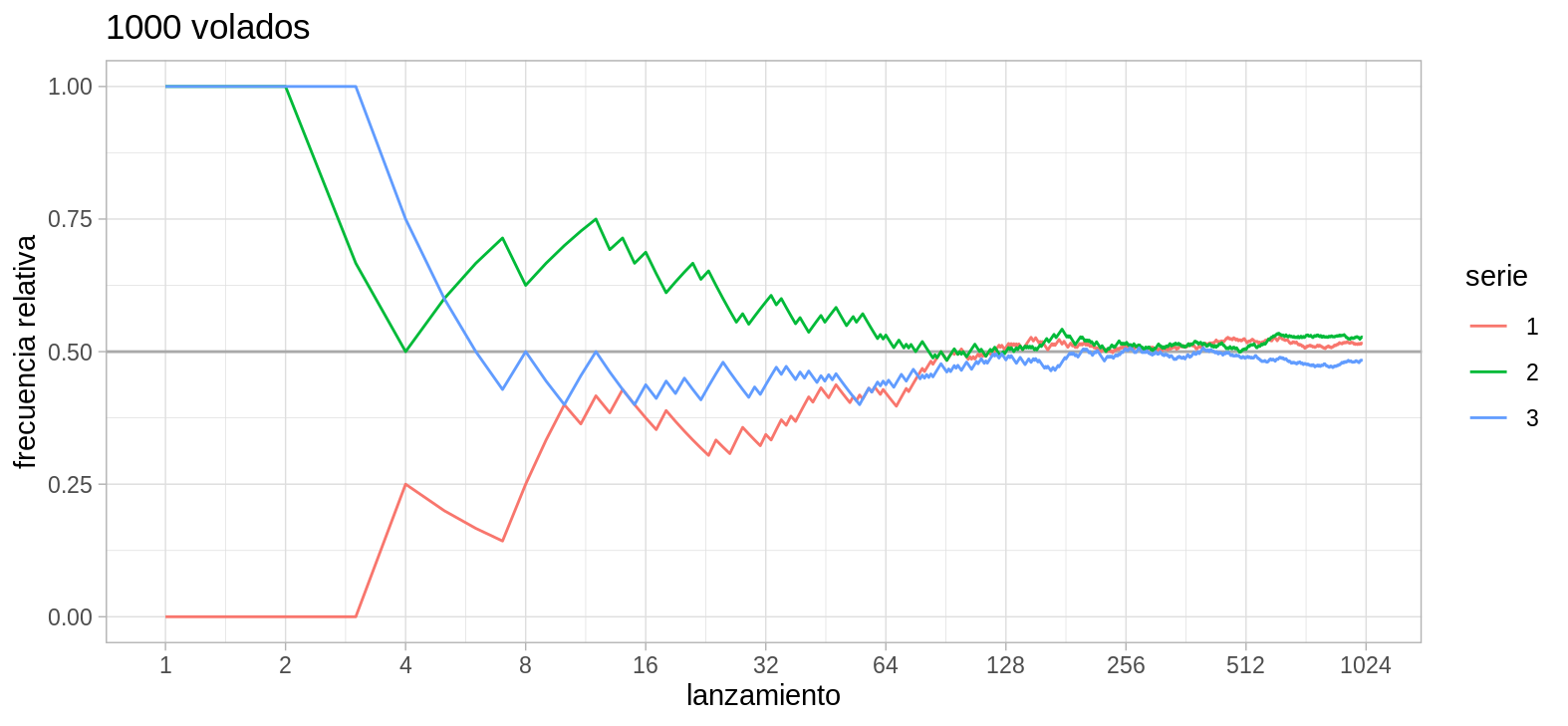
La segunda observación empírica es que, cuando el modelo de resultados equiprobables es apropiado:
- En el modelo de resultados equiprobables, la frecuencia relativa a largo plazo de ocurrencia de un evento es su probabilidad \(P(A)\) de ocurrencia
- Esta interpretación es crucial, pues es la única que realmente nos permite conectar nuestros modelos probabilísticos con observaciones empíricas.
Ejemplo: Lanzamiento de dos monedas
Supongamos que lanzamos dos monedas de manera simultánea. ¿Cuál es la probabilidad de que las dos monedas sean águila?
Las dos son águila o no, así que la posibilidad es 1/2.
Si definimos el resultado como el número de caras que se leen en las monedas, puede haber 0, 1 o 2. Si suponemos que estos tres resultados son igualmente probables, entonces la posibilidad es 1/3.
A pesar de que las monedas son similares supongamos que se pueden distinguir, llamémoslas moneda 1 y moneda 2. Ahora tenemos cuatro posibles resultados: AA, AS, SA, SS, (la primer letra corresponde a la cara observada en la moneda 1 y la segunda en la moneda 2). Si estos 4 resultados son igualmente probables entonces el evento AA tiene posibilidad de 1/4.
¿Cuál es la respuesta correcta?
En cuanto a teoría formal todas son correctas, cada escenario tiene supuestos de resultados equiprobables claramente enunciados y en base a éstos determina una probabilidad de manera correcta; sin embargo, los supuestos son diferentes y por tanto también las conclusiones. Únicamente una de las soluciones puede ser consistente con la interpretación frecuentista, ¿cuál es?
La primer respuesta es incorrecta pues supone probabilidad cero para el evento águila y sol. La solución dos, por otra parte, no es fácil de desacreditar, así que realicemos el experimento para encontrar la respuesta:
n <- 10000
moneda_1 <- sample(c("A", "S"), n, replace = TRUE)
moneda_2 <- sample(c("A", "S"), n, replace = TRUE)
sum(moneda_1 == moneda_2 & moneda_1 == "A") / n
#> [1] 0.2482La respuesta 3 es la correcta, y lo que vemos es que incluso cuando el supuesto de igualmente probables es apropiado a un cierto nivel de descripción determinado, este nivel no es algo que se pueda juzgar usando únicamente matemáticas, sino que se debe juzgar usando una interpretación de la probabilidad, como frecuencias relativas en ensayos. Más aún, hay ejemplos donde las monedas no son justas, o el sexo de un bebé recién nacido, donde el supuesto de equiprobabilidad no es adecuado.