10.12 Reparametrización
El muestreador de Stan puede ser muy lento cuando la geometría de la distribución posterior es complicada, una manera de acelerar la convergencia es reparametrizando.
Ejemplo: El embudo de Neal
Veamos como ejemplo el embudo de Neal, tomado de la guía de usuarios de Stan, Neal (2003) define una distribución en la que ejemplifica las dificultades de muestrear de modelos jerárquicos, es un ejemplo extremo pero es fácil ver como la reparametrización hace que el muestreo de la posterior se simplifique.
En este ejemplo la densidad es,
\[p(y,x)=normal(y|0,3)*\prod_{n=1}^9normal(x_n|0,exp(y/2))\]
Y las curvas de nivel de probabilidad tienen la forma de embudos de 10 dimensiones. El cuello de los embudos es muy estrecho por la transformación de la variable \(y\).
log_p_fun <- function(x, y) {
dnorm(y, 0, 3, log = TRUE) + dnorm(x, 0, exp(y / 2), log = TRUE)
}
grid_eval <- expand_grid(x = seq(-20, 20, by = 0.03),
y = seq(-9, 9, by = 0.03)) %>%
mutate(log_p = log_p_fun(x = x, y = y)) %>%
filter(log_p > -20)
head(grid_eval)
#> # A tibble: 6 x 3
#> x y log_p
#> <dbl> <dbl> <dbl>
#> 1 -20 2.58 -19.8
#> 2 -20 2.61 -19.3
#> 3 -20 2.64 -18.9
#> 4 -20 2.67 -18.5
#> 5 -20 2.70 -18.1
#> 6 -20 2.73 -17.8ggplot(grid_eval, aes(x, y, fill = log_p)) +
geom_raster() +
scale_fill_distiller(palette = "Spectral", direction = -1, na.value = NA,
name = expression(log(p(y, x["1"])))) +
ylim(-9, 9) +
xlim(-20, 20)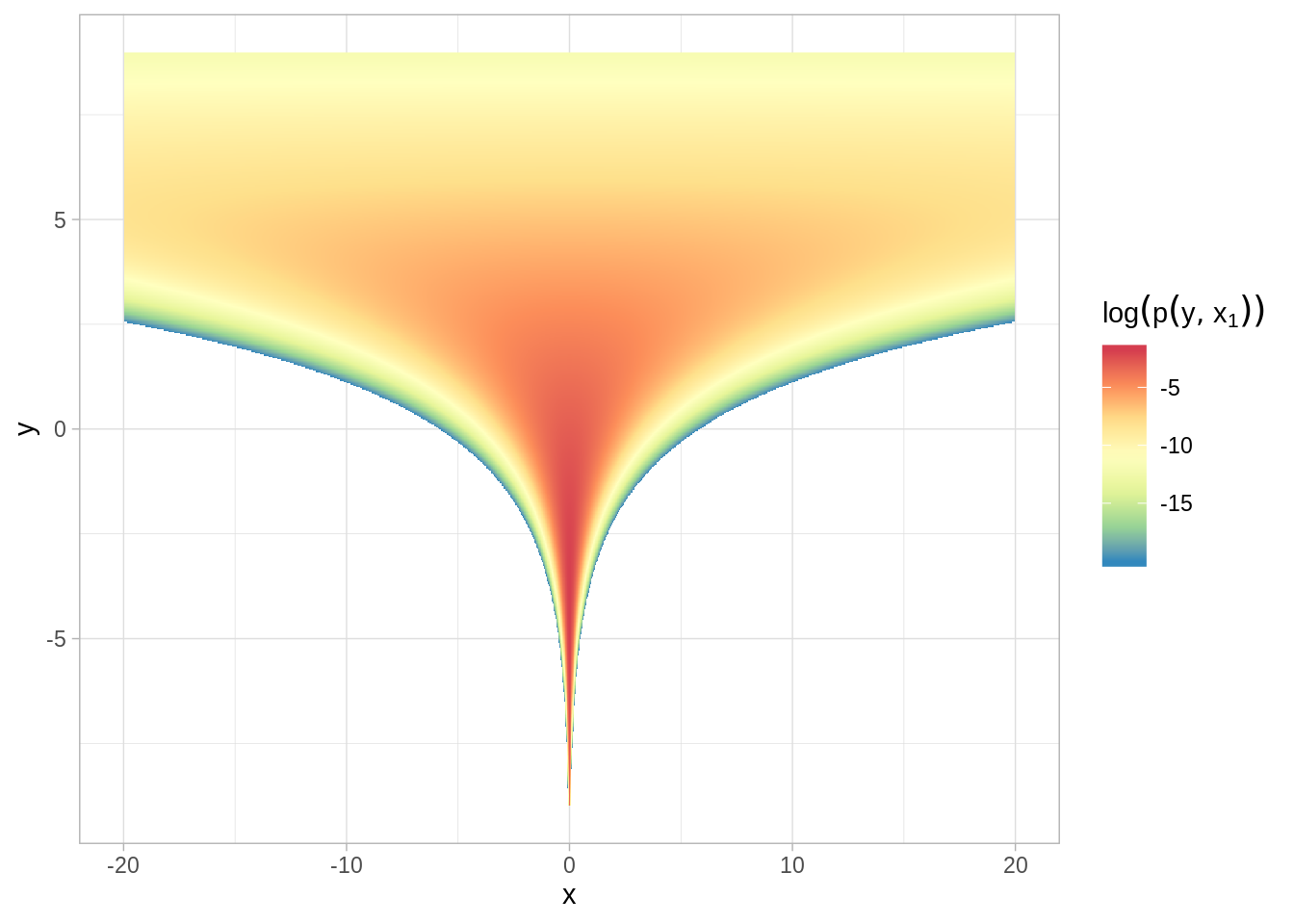
Y podemos implementar en Stan:
funnel.stan <-
'
parameters {
real y;
vector[9] x;
}
model {
y ~ normal(0, 3);
x ~ normal(0, exp(y/2));
}
'
cat(funnel.stan, file = "src/stan_files/funnel.stan")Cuando el modelo está expresado de esta manera, Stan tiene problemas para muestrear del cuello del embudo, pues cuando \(y\) es chica \(x\) está restringida a valores cercanos a cero, esto se debe a que la escala de la densidad cambia con \(y\) de tal manera que el tamaño de paso que funciona bien en el cuerpo de la densidad será muy grande en eñ cuello y viceversa, un tamaño de paso que funciona bien en el cuello será ineficiente en el cuerpo.
funnel_cpp <- stan_model("src/stan_files/funnel.stan")
funnel_sims <- sampling(object = funnel_cpp, chains = 3 , iter = 1000)
funnel_sims
#> Inference for Stan model: funnel.
#> 3 chains, each with iter=1000; warmup=500; thin=1;
#> post-warmup draws per chain=500, total post-warmup draws=1500.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> y 1.64 0.25 1.84 -1.30 0.24 1.48 2.89 5.49 52 1.02
#> x[1] 0.03 0.10 4.74 -9.02 -1.20 0.13 1.33 9.19 2043 1.00
#> x[2] 0.18 0.17 6.47 -9.72 -1.37 0.05 1.46 11.10 1437 1.00
#> x[3] 0.06 0.14 5.80 -10.75 -1.43 0.01 1.26 10.61 1809 1.00
#> x[4] 0.21 0.15 5.62 -10.09 -1.36 0.09 1.46 11.01 1323 1.00
#> x[5] 0.10 0.12 6.17 -9.23 -1.23 0.07 1.31 11.14 2519 1.00
#> x[6] 0.02 0.11 5.07 -9.56 -1.32 0.03 1.48 10.52 2220 1.00
#> x[7] 0.07 0.12 6.33 -10.69 -1.19 -0.06 1.29 9.75 2689 1.00
#> x[8] 0.04 0.12 5.50 -9.58 -1.31 -0.07 1.31 10.05 1986 1.00
#> x[9] 0.18 0.16 5.34 -9.96 -1.28 0.00 1.41 11.10 1179 1.00
#> lp__ -12.43 1.19 8.60 -31.12 -18.48 -11.37 -5.81 1.15 52 1.02
#>
#> Samples were drawn using NUTS(diag_e) at Tue Dec 10 23:28:38 2019.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).y <- extract(funnel_sims, "y")$y
x_1 <- extract(funnel_sims, "x[1]")$`x[1]`
sims_funnel <- tibble(y = y, x_1 = x_1)
ggplot(sims_funnel, aes(x_1, y)) +
geom_point(alpha = 0.5) +
ylim(-9, 9) +
xlim(-20, 20)
#> Warning: Removed 15 rows containing missing values (geom_point).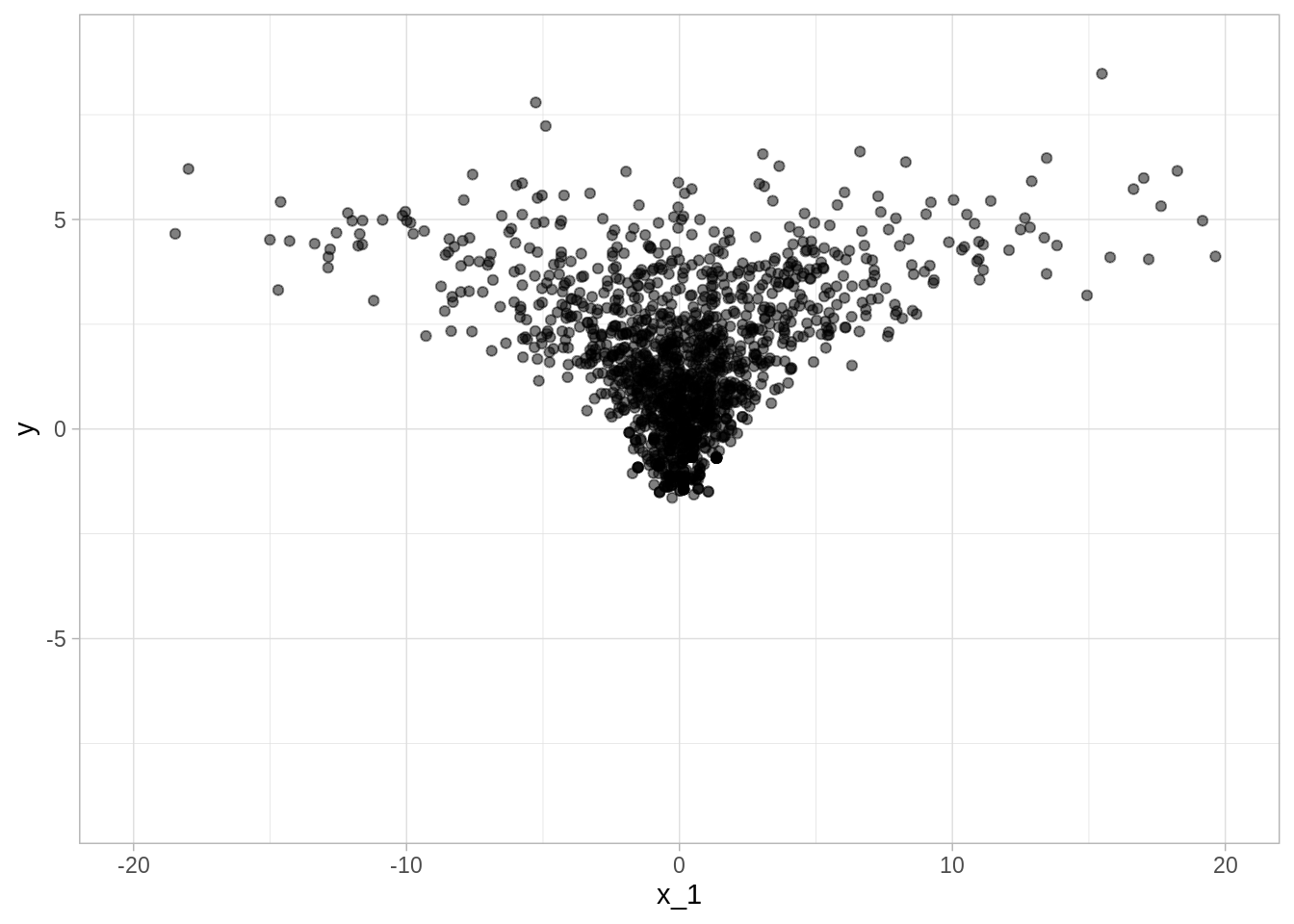
En este ejemplo particular podemos reparametrizar y escribir el modelo de la siguiente forma que hace el muestreador más eficiente:
no_funnel.stan <-
'
parameters {
real y_raw;
vector[9] x_raw;
}
transformed parameters {
real y;
vector[9] x;
y = 3.0 * y_raw;
x = exp(y/2) * x_raw;
}
model {
y_raw ~ std_normal(); // implies y ~ normal(0, 3)
x_raw ~ std_normal(); // implies x ~ normal(0, exp(y/2))
}
'
cat(no_funnel.stan, file = "src/stan_files/no_funnel.stan")En este segundo modelo, x_raw y y_raw se muestrean de manera independiente
de normales estándar, lo cuál es fácil para Stan. En un segundo paso se
transforman a muestras del embudo.
no_funnel_cpp <- stan_model("src/stan_files/no_funnel.stan")
no_funnel_sims <- sampling(object = no_funnel_cpp, chains = 3 , iter = 1000)
no_funnel_sims
#> Inference for Stan model: no_funnel.
#> 3 chains, each with iter=1000; warmup=500; thin=1;
#> post-warmup draws per chain=500, total post-warmup draws=1500.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> y_raw 0.01 0.02 0.98 -1.96 -0.63 0.01 0.68 1.87 2626 1.00
#> x_raw[1] -0.01 0.02 1.04 -2.10 -0.77 -0.01 0.69 1.99 2440 1.00
#> x_raw[2] 0.00 0.02 0.98 -1.91 -0.67 0.01 0.66 1.85 2237 1.00
#> x_raw[3] -0.02 0.02 0.97 -1.86 -0.68 -0.05 0.65 1.96 2489 1.00
#> x_raw[4] -0.01 0.02 1.01 -1.91 -0.72 -0.01 0.70 1.99 3252 1.00
#> x_raw[5] 0.02 0.02 1.02 -1.93 -0.65 0.00 0.70 1.99 2682 1.00
#> x_raw[6] 0.00 0.02 1.01 -1.97 -0.68 0.00 0.70 1.91 3389 1.00
#> x_raw[7] -0.01 0.02 1.01 -1.97 -0.70 0.00 0.63 2.03 3093 1.00
#> x_raw[8] 0.01 0.02 0.99 -1.89 -0.66 0.02 0.69 1.95 2651 1.00
#> x_raw[9] -0.02 0.02 1.00 -2.01 -0.71 0.00 0.67 1.88 2605 1.00
#> y 0.02 0.06 2.94 -5.89 -1.90 0.03 2.03 5.60 2626 1.00
#> x[1] 0.09 0.33 11.08 -9.60 -0.67 0.00 0.66 8.63 1110 1.00
#> x[2] 0.16 0.18 6.58 -8.21 -0.55 0.00 0.62 9.59 1300 1.00
#> x[3] -0.51 0.22 7.36 -10.37 -0.58 -0.01 0.51 7.33 1166 1.00
#> x[4] 0.01 0.17 6.03 -8.65 -0.65 0.00 0.57 9.26 1302 1.00
#> x[5] -0.39 0.34 10.42 -10.30 -0.58 0.00 0.59 9.04 916 1.00
#> x[6] 0.00 0.19 6.42 -9.02 -0.58 0.00 0.64 8.82 1171 1.00
#> x[7] -0.24 0.23 8.14 -11.23 -0.63 0.00 0.54 8.85 1283 1.00
#> x[8] -0.09 0.22 8.17 -8.58 -0.57 0.00 0.58 9.51 1359 1.00
#> x[9] -0.10 0.29 10.12 -9.66 -0.58 0.00 0.57 10.03 1190 1.00
#> lp__ -5.00 0.09 2.25 -10.44 -6.25 -4.66 -3.31 -1.75 617 1.01
#>
#> Samples were drawn using NUTS(diag_e) at Tue Dec 10 23:29:28 2019.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).y <- extract(no_funnel_sims, "y")$y
x_1 <- extract(no_funnel_sims, "x[1]")$`x[1]`
sims_no_funnel <- tibble(y = y, x_1 = x_1)
ggplot(sims_no_funnel, aes(x_1, y)) +
geom_point(alpha = 0.5) +
ylim(-9, 9) +
xlim(-20, 20)
#> Warning: Removed 26 rows containing missing values (geom_point).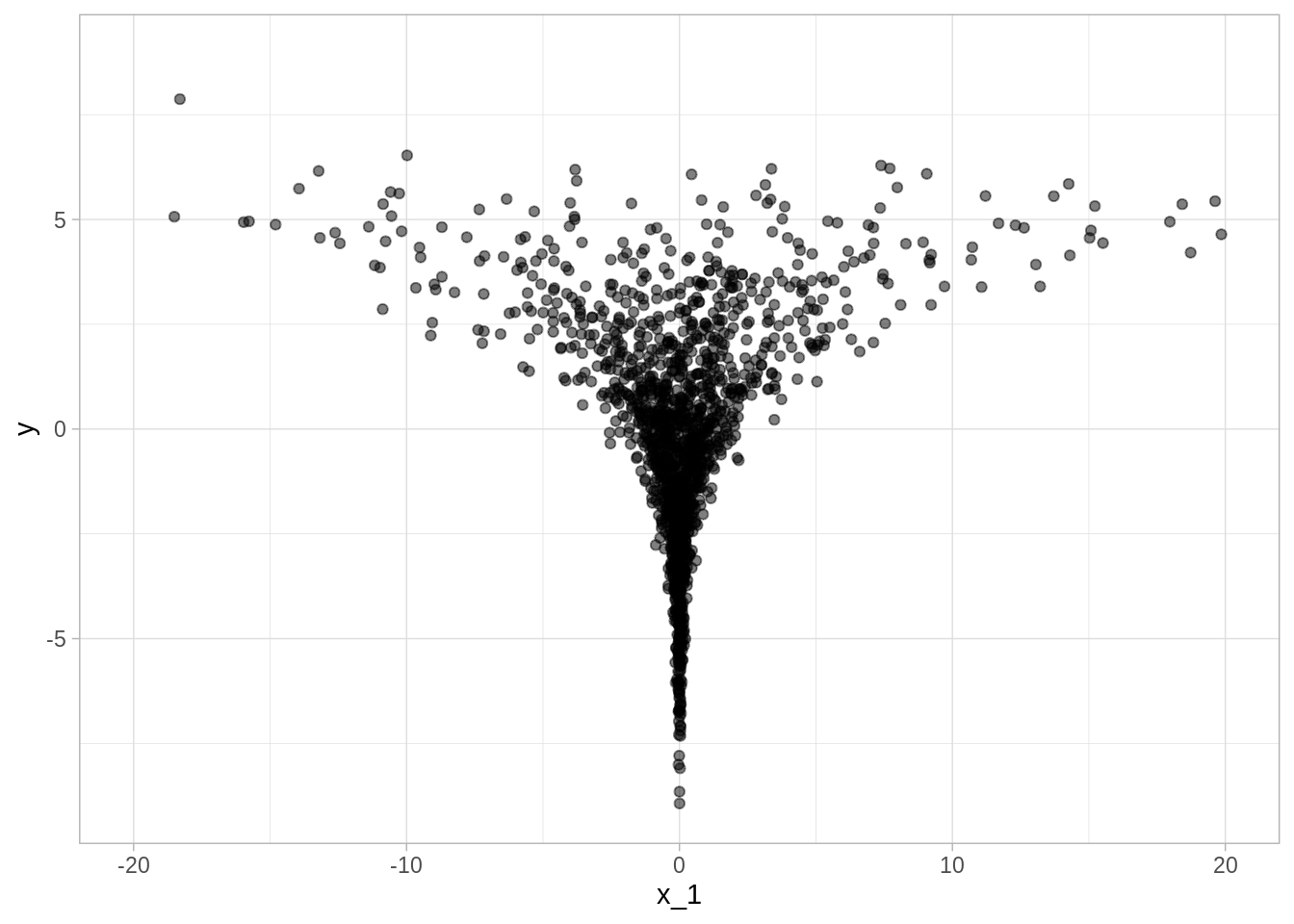
Modelos jerárquicos y parametrización no centrada
En modelos jerárquicos es común encontrarse con geometrías complejas, una parametrización que suele ayudar para acelerar convergencia es la parametrización no centrada.
Parametrización centrada
Un modelo jerárquico usual seleccionaría muestras de un vector de coeficientes \(\beta\) como sigue:
parameters {
real mu_beta;
real<lower=0> sigma_beta;
vector[K] beta;
...
model {
beta ~ normal(mu_beta, sigma_beta);
...Y tendría ineficiencias como el embudo de Neal, debido a que el valor de \(\beta\) (vector), \(\mu_{\beta}\) y \(\sigma_{\beta}\) tienen alta correlación en la posterior. El nivel de correlación dependerá de la cantidad de datos disponibles siendo mayor cuanto menos información se tenga. En estos casos, de datos limitados, es más eficiente usar una parametrización no centrada.
Parametrización no centrada
parameters {
vector[K] beta_raw;
...
transformed parameters {
vector[K] beta;
// implies: beta ~ normal(mu_beta, sigma_beta)
beta = mu_beta + sigma_beta * beta_raw;
model {
beta_raw ~ std_normal();
...Las iniciales de mu_beta y sigma_beta permanecen sin cambios respecto al
modelo original.
Ahora veremos un ejemplo práctivo de parametrización no centrada en un modelo de predicción de resultados del conteo rápido, que además ejemplifica un flujo de trabajo bayesiano, con pasos de ajuste, inferencia, calibración y evaluación de robustez. El ejemplo está en esta liga.