10. Simulación muestra y bootstrap paramétrico
Simulación para calcular tamaños de muestra
Supongamos que queremos hacer una encuesta para estimar la proporción de hogares donde se consume refresco de manera regular, para ello se diseña un muestreo por conglomerados donde los conglomerados están dados por conjuntos de hoagres de tal manera que todos los conglomerados tienen el mismo número de hogares. La selección de la muestra se hará en dos etapas:
Seleccionamos \(J\) conglomerados de manera aleatoria.
En cada conglomerado seleccionames \(n/J\) hogares para entrevistar.
El estimador será simplemente el porcentaje de hogares del total de la muestra que consume refresco. Suponemos que la verdadera proporción es cercana a \(0.50\) y que la media de la proporción de interés tiene una desviación estándar de \(0.1\) a lo largo de los conglomerados .
Supongamos que la muestra total es de \(n=1000\). ¿Cuál es la estimación del error estándar para la proporción estimada si \(J=1,10,100,1000\)?
El obejtivo es estimar la propoción que consume refresco en la población con un error estándar de a lo más \(2\%\). ¿Que valores de \(J\) y \(n\) debemos elegir para cumplir el objetivo al menor costo?
Los costos del levantamiento son: + \(50\) pesos por encuesta. + \(500\) pesos por conglomerado
Solución
muestreo <- function(J, n_total = 1000) {
n_cong <- floor(n_total / J)
medias <- rnorm(J, 0.5, 0.1)
medias <- case_when(
medias < 0 ~ 0,
medias > 1 ~ 1,
TRUE ~ medias)
resp <- rbinom(J, n_cong, medias)
sum(resp) / n_total
}
errores <- tibble(J = c(1, 10, 100, 1000)) %>%
mutate(sims = map(J, ~(rerun(1000, muestreo(.)) %>%
flatten_dbl())),
error_est = map_dbl(sims, sd) %>% round(3))
errores
#> # A tibble: 4 x 3
#> J sims error_est
#> <dbl> <list> <dbl>
#> 1 1 <dbl [1,000]> 0.098
#> 2 10 <dbl [1,000]> 0.035
#> 3 100 <dbl [1,000]> 0.02
#> 4 1000 <dbl [1,000]> 0.016
tamano_muestra <- function(J) {
n_total <- max(100, J)
ee <- rerun(500, muestreo(J = J, n_total = n_total)) %>%
flatten_dbl() %>% sd()
while(ee > 0.02){
n_total = n_total + 20
ee <- rerun(500, muestreo(J = J, n_total = n_total)) %>%
flatten_dbl() %>%
sd() %>%
round(3)
}
list(ee = ee, n_total = n_total, costo = 500 * J + 50 * n_total)
}
tamanos <- c(20, 30, 40, 50, 100, 150)
costos <- map_df(tamanos, tamano_muestra)
costos$J <- tamanos
costos
#> # A tibble: 6 x 4
#> ee n_total costo J
#> <dbl> <dbl> <dbl> <dbl>
#> 1 0.02 23000 1160000 20
#> 2 0.02 1900 110000 30
#> 3 0.02 1100 75000 40
#> 4 0.02 940 72000 50
#> 5 0.02 580 79000 100
#> 6 0.019 550 102500 150
ggplot(costos, aes(x = J, y = costo / 1000)) +
geom_line() + scale_y_log10() + theme_minimal() +
labs(y = "miles de pesos", title = "Costos")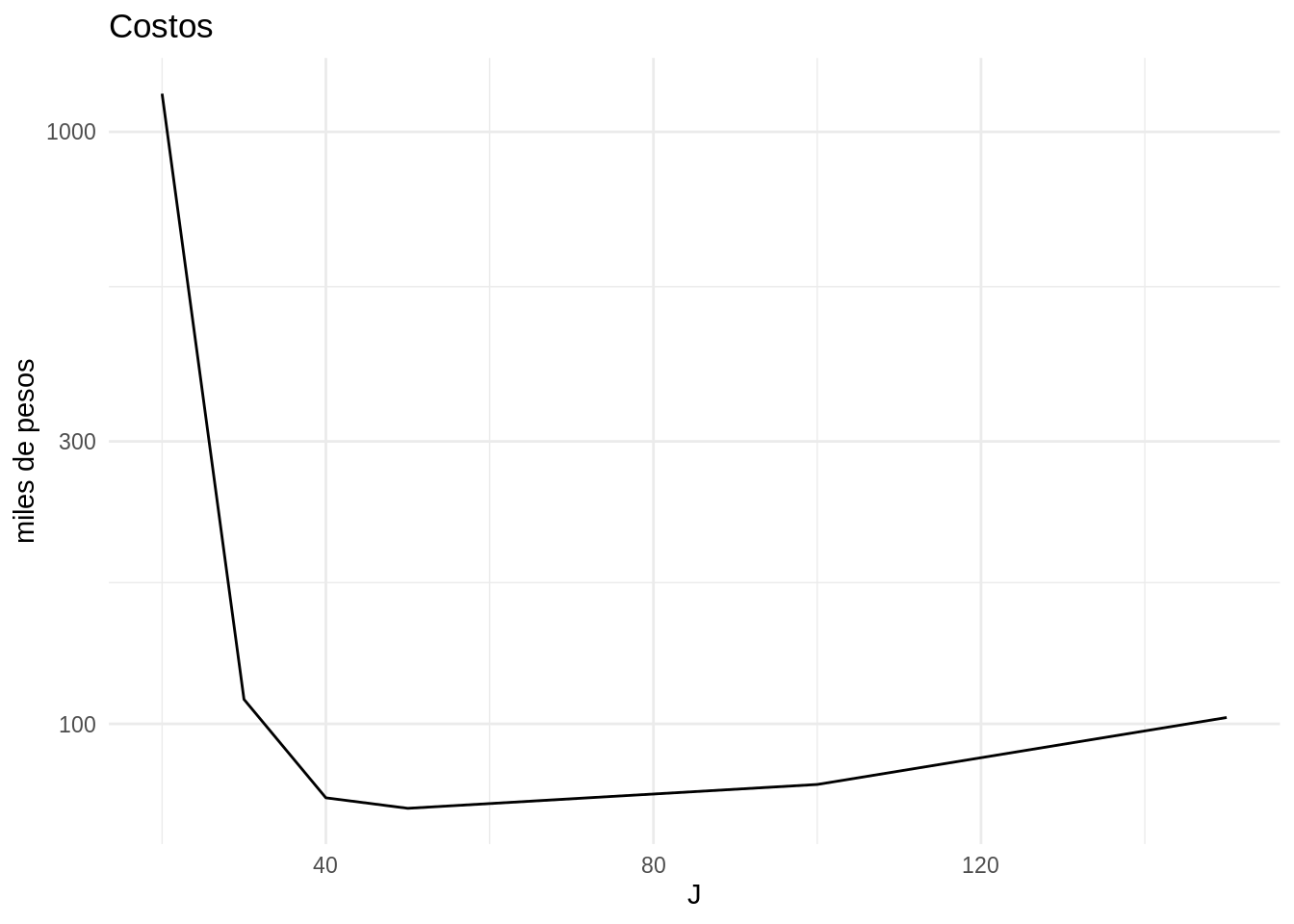
Bootstrap paramétrico
- Sean \(X_1,...,X_n \sim N(\mu, 1)\). Sea \(\theta = e^{\mu}\), simula una muestra de \(n=100\) observaciones usando \(\mu=5\).
Usa el método delta para estimar \(\hat{se}\) de \(\hat{\theta}\) y crea un intervalo del \(95\%\) de confianza. Pista: \(se(\hat{\mu}) = 1/\sqrt{n}\)
Repite el inciso anterior usando boostrap paramétrico.
Finalmente usa bootstrap no paramétrico y compara tus respuestas.
Realiza un histograma de replicaciones bootstrap para cada método, estas son estimaciones de la distribución de \(\hat{\theta}\). El método delta también nos da una aproximación a esta distribución: \(Normal(\hat{\theta},\hat{se}^2)\). Comparalos con la verdadera distribución de \(\hat{\theta}\) (que puedes obtener vía simulación). ¿Cuál es la aproximación más cercana a la verdadera distribución?