4. Programación funcional y distribución muestral

Descarga la carpeta specdata, ésta contiene 332 archivos csv que almacenan información de monitoreo de contaminación en 332 ubicaciones de EUA. Cada archivo contiene información de una unidad de monitoreo y el número de identificación del monitor es el nombre del archivo. En este ejercicio nos interesa unir todas las tablas en un solo data.frame que incluya el identificador de las estaciones.

La siguiente instrucción descarga los datos si trabajas con proyectos de RStudio, también puedes descargar el zip manualmente.

library(usethis)
use_directory("data") 
use_zip("https://d396qusza40orc.cloudfront.net/rprog%2Fdata%2Fspecdata.zip", 
    destdir = "data")

Crea un vector con las direcciones de los archivos.
Lee uno de los archivos usando la función read_csv() del paquete readr.
Tip: especifica el tipo de cada columna usando el parámetro col_types.
Utiliza la función map_df() para iterar sobre el vector con las direcciones de los archivos csv y crea un data.frame con todos los datos, recuerda añadir una columna con el nombre del archivo para poder identificar la estación.

Consideramos los datos de ENLACE edo. de México (enlace), y la columna de calificaciones de español 3^o de primaria (esp_3).

library(estcomp)
enlace <- enlacep_2013 %>% 
    janitor::clean_names() %>% 
    mutate(id = 1:n()) %>% 
    select(id, cve_ent, turno, tipo, esp_3 = punt_esp_3, esp_6 = punt_esp_6, 
        n_eval_3 = alum_eval_3, n_eval_6 = alum_eval_6) %>% 
    na.omit() %>% 
    filter(esp_3 > 0, esp_6 > 0, n_eval_3 > 0, n_eval_6 > 0, cve_ent == "15")

Selecciona una muestra de tamaño \(n = 10, 100, 1000\). Para cada muestra calcula media y el error estándar de la media usando el principio del plug-in: \(\hat{\mu}=\bar{x}\), y \(\hat{se}(\bar{x})=\hat{\sigma}_{P_n}/\sqrt{n}\). Tip: Usa la función sample_n() del paquete deplyr para generar las muestras.
Ahora aproximareos la distribución muestral, para cada tamaño de muestra \(n\):

simula \(10,000\) muestras aleatorias, ii) calcula la media en cada muestra,
Realiza un histograma de la distribución muestral de las medias (las medias del paso anterior) iv) aproxima el error estándar calculando la desviación estándar de las medias del paso ii. Tip: Escribe una función que dependa del tamaño de muestra y usa la función rerun() del paquete purrr para hacer las \(10,000\) simulaciones.

simula_media <- function(n) {
    
}
medias_10 <- rerun(10000, simula_media(n = 10)) %>% flatten_dbl()

Calcula el error estándar de la media para cada tamaño de muestra usando la información poblacional (ésta no es una aproximación), usa la fórmula: \(se_P(\bar{x}) = \sigma_P/ \sqrt{n}\).
¿Cómo se comparan los errores estándar correspondientes a los distintos tamaños de muestra?

Solución + bootstrap

Presentamos la solución del ejercicio y agregamos como haríamos con bootsrtap.

Suponemos que me interesa hacer inferencia del promedio de las calificaciones de los estudiantes de tercero de primaria en el Estado de México.

En este ejercicio planteamos \(3\) escenarios (que simulamos): 1) que tengo una muestra de tamaño \(10\), 2) que tengo una muestra de tamaño \(100\), y 3) que tengo una muestra de tamaño \(1000\).

Selección de muestras:

set.seed(373783326)
muestras <- tibble(tamanos = c(10, 100, 1000)) %>% 
    mutate(muestras = map(tamanos, ~sample(enlace$esp_3, size = .)))

Ahora procedemos de manera usual en estadística (usando fórmulas y no simulación), estimo la media de la muestra con el estimador plug-in \[\bar{x}={1/n\sum x_i}\] y el error estándar de \(\bar{x}\) con el estimador plug-in \[\hat{se}(\bar{x}) =\bigg\{\frac{1}{n^2}\sum_{i=1}^n(x_i-\bar{x})^2\bigg\}^{1/2}\]

Estimadores plug-in:

se_plug_in <- function(x){
    x_bar <- mean(x)
    n_x <- length(x)
    var_x <- 1 / n_x ^ 2 * sum((x - x_bar) ^ 2)
    sqrt(var_x)
}
muestras_est <- muestras %>% 
    mutate(
        medias = map_dbl(muestras, mean), 
        e_estandar_plug_in = map_dbl(muestras, se_plug_in)
    )
muestras_est
#> # A tibble: 3 x 4
#>   tamanos muestras      medias e_estandar_plug_in
#>     <dbl> <list>         <dbl>              <dbl>
#> 1      10 <dbl [10]>      602.              19.3 
#> 2     100 <dbl [100]>     553.               6.54
#> 3    1000 <dbl [1,000]>   552.               1.90

Ahora, recordemos que la distribución muestral es la distribución de una estadística, considerada como una variable aleatoria. Usando esta definción podemos aproximarla, para cada tamaño de muestra, simulando:

simulamos muestras de tamaño \(n\) de la población,
calculamos la estadística de interés (en este caso \(\bar{x}\)),
vemos la distribución de la estadística a lo largo de simulaciones.

Histogramas de distribución muestral y aproximación de errores estándar con simulación

muestras_sims <- muestras_est %>%
    mutate(
        sims_muestras = map(tamanos, ~rerun(10000, sample(enlace$esp_3, 
            size = ., replace = TRUE))), 
        sims_medias = map(sims_muestras, ~map_dbl(., mean)), 
        e_estandar_aprox = map_dbl(sims_medias, sd)
        )
sims_medias <- muestras_sims %>% 
    select(tamanos, sims_medias) %>% 
    unnest(sims_medias) 

ggplot(sims_medias, aes(x = sims_medias)) +
    geom_histogram(binwidth = 2) +
    facet_wrap(~tamanos, nrow = 1) +
    theme_minimal()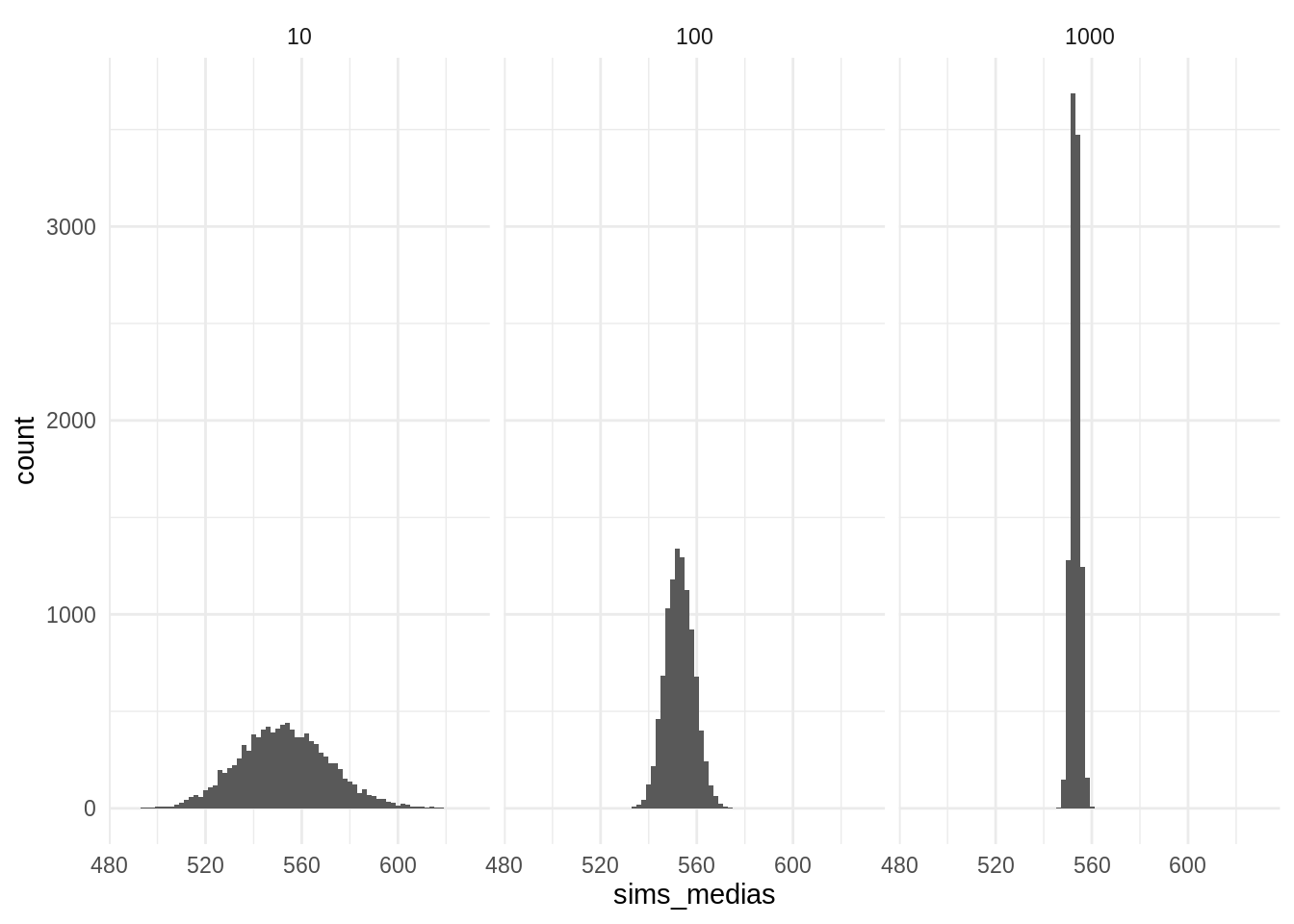

Notamos que la variación en la distribución muestral decrece conforme aumenta el tamaño de muestra, esto es esperado pues el error estándar de una media es \(\sigma_P / \sqrt{n}\), y dado que en este ejemplo estamos calculando la media para la misma población el valor poblacional \(\sigma_P\) es constante y solo cambia el denominador.

Nuestros valores de error estándar con simulación están en la columna e_estandar_aprox:

muestras_sims %>% 
    select(tamanos, medias, e_estandar_plug_in, e_estandar_aprox)
#> # A tibble: 3 x 4
#>   tamanos medias e_estandar_plug_in e_estandar_aprox
#>     <dbl>  <dbl>              <dbl>            <dbl>
#> 1      10   602.              19.3             18.9 
#> 2     100   553.               6.54             5.92
#> 3    1000   552.               1.90             1.87

En este ejercicio estamos simulando para examinar las distribuciones muestrales y para ver que podemos aproximar el error estándar de la media usando simulación; sin embargo, dado que en este caso hipotético conocemos la varianza poblacional y la fórmula del error estándar de una media, por lo que podemos calcular el verdadero error estándar para una muestra de cada tamaño.

Calcula el error estándar de la media para cada tamaño de muestra usando la información poblacional:

muestras_sims_est <- muestras_sims %>% 
    mutate(e_estandar_pob = sd(enlace$esp_3) / sqrt(tamanos))
muestras_sims_est %>% 
    select(tamanos, e_estandar_plug_in, e_estandar_aprox, e_estandar_pob)
#> # A tibble: 3 x 4
#>   tamanos e_estandar_plug_in e_estandar_aprox e_estandar_pob
#>     <dbl>              <dbl>            <dbl>          <dbl>
#> 1      10              19.3             18.9           18.7 
#> 2     100               6.54             5.92           5.93
#> 3    1000               1.90             1.87           1.87

En la tabla de arriba podemos comparar los \(3\) errores estándar que calculamos, recordemos que de estos \(3\) el plug-in es el único que podríamos obtener en un escenario real pues los otros dos los calculamos usando la población.

Una alternativa al estimador plug-in del error estándar es usar bootstrap (en muchos casos no podemos calcular el error estándar plug-in por falta de fórmulas) pero podemos usar bootstrap: utilizamos una estimación de la distribución poblacional y calculamos el error estándar bootstrap usando simulación. Hacemos el mismo procedimiento que usamos para calcular e_estandar_apox pero sustituimos la distribución poblacional por la distriución empírica. Hagámoslo usando las muestras que sacamos en el primer paso:

muestras_sims_est_boot <- muestras_sims_est %>% 
    mutate(
        sims_muestras_boot = map2(muestras, tamanos,
            ~rerun(10000, sample(.x, size = .y, replace = TRUE))), 
        sims_medias_boot = map(sims_muestras_boot, ~map_dbl(., mean)), 
        e_estandar_boot = map_dbl(sims_medias_boot, sd)
        )
muestras_sims_est_boot
#> # A tibble: 3 x 11
#>   tamanos muestras medias e_estandar_plug… sims_muestras sims_medias
#>     <dbl> <list>    <dbl>            <dbl> <list>        <list>     
#> 1      10 <dbl [1…   602.            19.3  <list [10,00… <dbl [10,0…
#> 2     100 <dbl [1…   553.             6.54 <list [10,00… <dbl [10,0…
#> 3    1000 <dbl [1…   552.             1.90 <list [10,00… <dbl [10,0…
#> # … with 5 more variables: e_estandar_aprox <dbl>, e_estandar_pob <dbl>,
#> #   sims_muestras_boot <list>, sims_medias_boot <list>, e_estandar_boot <dbl>

Graficamos los histogramas de la distribución bootstrap para cada muestra.

sims_medias_boot <- muestras_sims_est_boot %>% 
    select(tamanos, sims_medias_boot) %>% 
    unnest(sims_medias_boot) 

ggplot(sims_medias_boot, aes(x = sims_medias_boot)) +
    geom_histogram(binwidth = 4) +
    facet_wrap(~tamanos, nrow = 1) +
    theme_minimal()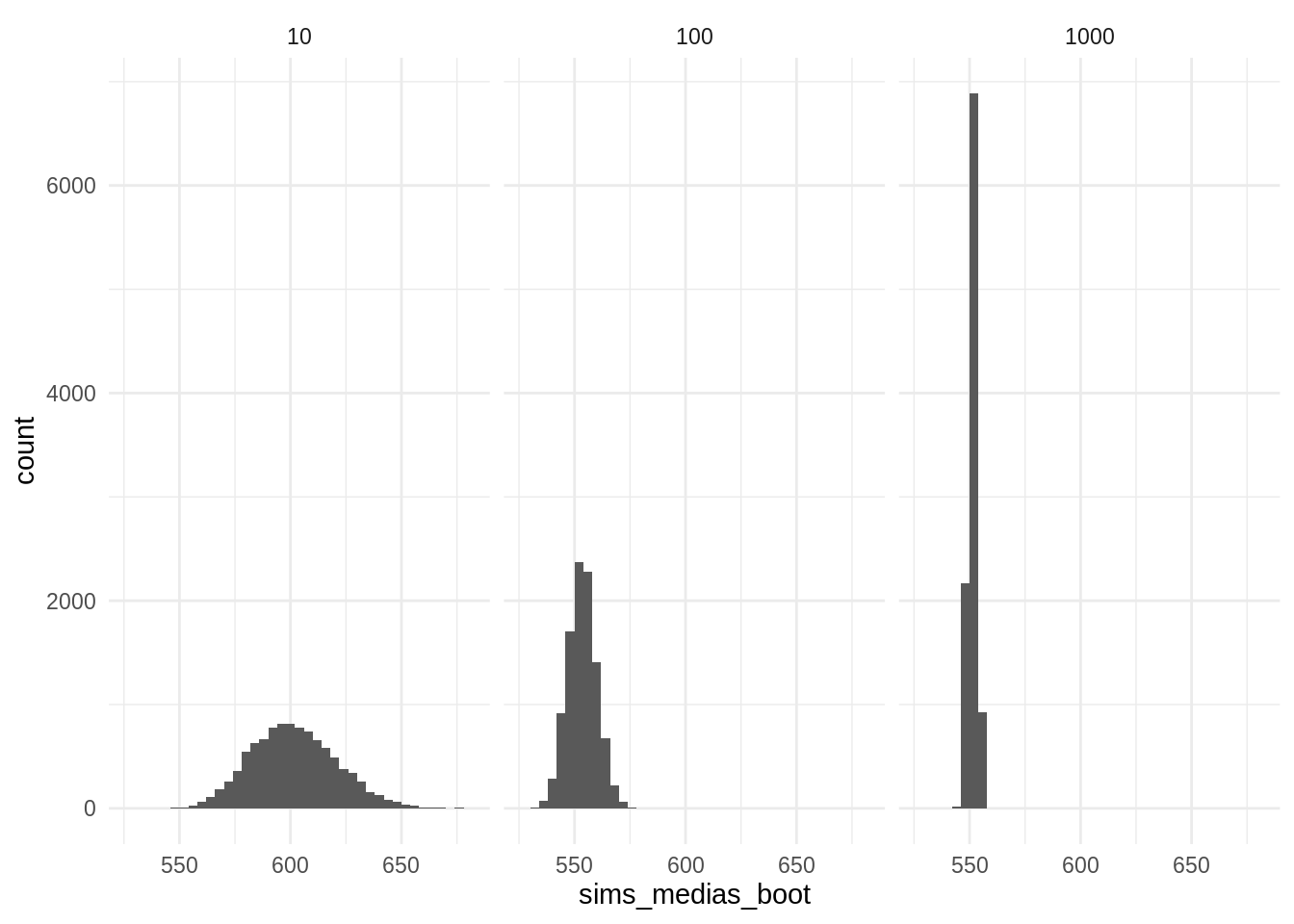

Y la tabla con todos los errores estándar quedaría:

muestras_sims_est_boot %>% 
    select(tamanos, e_estandar_boot, e_estandar_plug_in, e_estandar_aprox, 
        e_estandar_pob)
#> # A tibble: 3 x 5
#>   tamanos e_estandar_boot e_estandar_plug_in e_estandar_aprox e_estandar_pob
#>     <dbl>           <dbl>              <dbl>            <dbl>          <dbl>
#> 1      10           19.3               19.3             18.9           18.7 
#> 2     100            6.53               6.54             5.92           5.93
#> 3    1000            1.89               1.90             1.87           1.87

Observamos que el estimador bootstrap del error estándar es muy similar al estimador plug-in del error estándar, esto es esperado pues se calcularon con la misma muestra y el error estándar bootstrap converge al plug-in conforme incrementamos el número de muestras bootstrap.