7.1 Números pseudoaleatorios
El objetivo es generar sucesiones \(\{u_i\}_{i=1}^N\) de números independientes que se puedan considerar como observaciones de una distribución uniforme en el intervalo \((0, 1)\).
- Verdaderos números aleatorios. Los números completamente aleatorios (no
determinísticos) son fáciles de imaginar conceptualmente, por ejemplo
podemos imaginar lanzar una moneda, lanzar un dado o una lotería.
En general los números aleatorios se basan en alguna fuente de aleatoreidad física que puede ser teóricamente impredecible (cuántica) o prácticamente impredecible (caótica). Por ejemplo:- random.org genera aleatoreidad a través de ruido
atmosférico (el paquete
randomcontiene funciones para obtener números de random.org),
- ERNIE, usa ruido
térmico en transistores y se utiliza en la lotería de bonos de Reino Unido.
- RAND Corporation En 1955 publicó una tabla de un millón de números aleatorios que fue ampliamente utilizada. Los números en la tabla se obtuvieron de una ruleta electrónica.
- random.org genera aleatoreidad a través de ruido
atmosférico (el paquete
- Números pseudoaleatorios. Los números pseudoaleatorios se generan de
manera secuencial con un algoritmo determinístico, formalmente se definen
por:
- Función de inicialización. Recibe un número (la semilla) y pone al generador en su estado inicial.
- Función de transición. Transforma el estado del generador.
- Función de salidas. Transforma el estado para producir un número fijo de bits (0 ó 1).
Esto implica, entre otras cosas, que una sucesión de números pseudoaletorios esta completamente determinada por la semilla.
Ahora, buscamos que una secuencia de números pseudoaleatorios:
no muestre ningún patrón o regularidad aparente desde un punto de vista estadístico, y
dada una semilla inicial, se puedan generar muchos valores antes de repetir el ciclo.
Construir un buen algoritmo de números pseudoaleatorios es complicado, como veremos en los siguientes ejemplos.
Ejemplo: método de la parte media del cuadrado
En 1946 Jon Von Neuman sugirió usar las operaciones aritméticas de una computadora para generar secuencias de número pseudoaleatorios.
Sugirió el método middle square, para generar secuencias de dígitos pseudoaleatorios de 4 dígitos propuso,
Se inicia con una semilla de 4 dígitos:
seed = 9731La semilla se eleva al cuadrado, produciendo un número de 8 dígitos (si el resultado tiene menos de 8 dígitos se añaden ceros al inicio):
value = 94692361Los 4 números del centro serán el siguiente número en la secuencia, y se devuelven como resultado:
value = 6923
mid_square <- function(seed, n) {
seeds <- numeric(n)
values <- numeric(n)
for (i in 1:n) {
x <- seed ^ 2
seed = case_when(
nchar(x) > 2 ~ (x %/% 1e2) %% 1e4,
TRUE ~ 0)
values[i] <- x
seeds[i] <- seed
}
cbind(seeds, values)
}
x <- mid_square(1931, 10)
print(x, digits = 4)
#> seeds values
#> [1,] 7287 3728761
#> [2,] 1003 53100369
#> [3,] 60 1006009
#> [4,] 36 3600
#> [5,] 12 1296
#> [6,] 1 144
#> [7,] 0 1
#> [8,] 0 0
#> [9,] 0 0
#> [10,] 0 0
x <- mid_square(9731, 100)
print(x, digits = 4)
#> seeds values
#> [1,] 6923 94692361
#> [2,] 9279 47927929
#> [3,] 998 86099841
#> [4,] 9960 996004
#> [5,] 2016 99201600
#> [6,] 642 4064256
#> [7,] 4121 412164
#> [8,] 9826 16982641
#> [9,] 5502 96550276
#> [10,] 2720 30272004
#> [11,] 3984 7398400
#> [12,] 8722 15872256
#> [13,] 732 76073284
#> [14,] 5358 535824
#> [15,] 7081 28708164
#> [16,] 1405 50140561
#> [17,] 9740 1974025
#> [18,] 8676 94867600
#> [19,] 2729 75272976
#> [20,] 4474 7447441
#> [21,] 166 20016676
#> [22,] 275 27556
#> [23,] 756 75625
#> [24,] 5715 571536
#> [25,] 6612 32661225
#> [26,] 7185 43718544
#> [27,] 6242 51624225
#> [28,] 9625 38962564
#> [29,] 6406 92640625
#> [30,] 368 41036836
#> [31,] 1354 135424
#> [32,] 8333 1833316
#> [33,] 4388 69438889
#> [34,] 2545 19254544
#> [35,] 4770 6477025
#> [36,] 7529 22752900
#> [37,] 6858 56685841
#> [38,] 321 47032164
#> [39,] 1030 103041
#> [40,] 609 1060900
#> [41,] 3708 370881
#> [42,] 7492 13749264
#> [43,] 1300 56130064
#> [44,] 6900 1690000
#> [45,] 6100 47610000
#> [46,] 2100 37210000
#> [47,] 4100 4410000
#> [48,] 8100 16810000
#> [49,] 6100 65610000
#> [50,] 2100 37210000
#> [51,] 4100 4410000
#> [52,] 8100 16810000
#> [53,] 6100 65610000
#> [54,] 2100 37210000
#> [55,] 4100 4410000
#> [56,] 8100 16810000
#> [57,] 6100 65610000
#> [58,] 2100 37210000
#> [59,] 4100 4410000
#> [60,] 8100 16810000
#> [61,] 6100 65610000
#> [62,] 2100 37210000
#> [63,] 4100 4410000
#> [64,] 8100 16810000
#> [65,] 6100 65610000
#> [66,] 2100 37210000
#> [67,] 4100 4410000
#> [68,] 8100 16810000
#> [69,] 6100 65610000
#> [70,] 2100 37210000
#> [71,] 4100 4410000
#> [72,] 8100 16810000
#> [73,] 6100 65610000
#> [74,] 2100 37210000
#> [75,] 4100 4410000
#> [76,] 8100 16810000
#> [77,] 6100 65610000
#> [78,] 2100 37210000
#> [79,] 4100 4410000
#> [80,] 8100 16810000
#> [81,] 6100 65610000
#> [82,] 2100 37210000
#> [83,] 4100 4410000
#> [84,] 8100 16810000
#> [85,] 6100 65610000
#> [86,] 2100 37210000
#> [87,] 4100 4410000
#> [88,] 8100 16810000
#> [89,] 6100 65610000
#> [90,] 2100 37210000
#> [91,] 4100 4410000
#> [92,] 8100 16810000
#> [93,] 6100 65610000
#> [94,] 2100 37210000
#> [95,] 4100 4410000
#> [96,] 8100 16810000
#> [97,] 6100 65610000
#> [98,] 2100 37210000
#> [99,] 4100 4410000
#> [100,] 8100 16810000Este generador cae rápidamente en ciclos cortos, por ejemplo, si aparece un cero se propagará por siempre.
A inicios de 1950s se exploró el método y se propusieron mejoras, por ejemplo para evitar caer en cero. Metrópolis logró obtener una secuencia de 750,000 números distintos al usar semillas de 38 bits (usaba sistema binario), además la secuencia de Metrópolis mostraba propiedades deseables. No obstante, el método del valor medio no es considerado un método bueno por lo común de los ciclos cortos.
Ejemplo: rand
Por muchos años (antes de 1995) el generador de la función rand en Matlab fue el generador congruencial:
\[X_{n+1} = (7^5)X_n mod(2^{31}-1)\] Construyamos sucesiones de longitud \(1,500\) usando el algoritmo de rand:
sucesion <- function(n = 1500, semilla = runif(1, 0, 2 ^ 31 - 1)){
x <- rep(NA, n)
u <- rep(NA, n)
x[1] <- semilla
u[1] <- x[1] / (2 ^ 31 - 1) # transformamos al (0, 1)
for (i in 2:n) {
x[i] <- (7 ^ 5 * x[i - 1]) %% (2 ^ 31 - 1)
u[i] <- x[i] / (2 ^ 31 - 1)
}
u
}
u_rand <- sucesion(n = 150000)
sucesiones <- map_df(1:12, ~tibble(serie = ., sim = sucesion(),
ind = 1:length(sim)))
sucesiones
#> # A tibble: 18,000 x 3
#> serie sim ind
#> <int> <dbl> <int>
#> 1 1 0.637 1
#> 2 1 0.370 2
#> 3 1 0.688 3
#> 4 1 0.904 4
#> 5 1 0.691 5
#> 6 1 0.487 6
#> 7 1 0.614 7
#> 8 1 0.350 8
#> 9 1 0.989 9
#> 10 1 0.148 10
#> # … with 17,990 more rowsUna propiedad deseable es que la sucesión de \(u_i\) parezca una sucesión de observaciones independientes de una \(Uniforme(0,1)\).
- Veamos una gráfica del índice de simulación contra el valor obtenido
ggplot(sucesiones, aes(x = ind, y = sim)) +
geom_point(alpha = 0.5, size = 1.5) + # alpha controla la transparencia
facet_wrap(~ serie) +
geom_smooth(method = "loess", se = FALSE, color = "white", size = 0.7)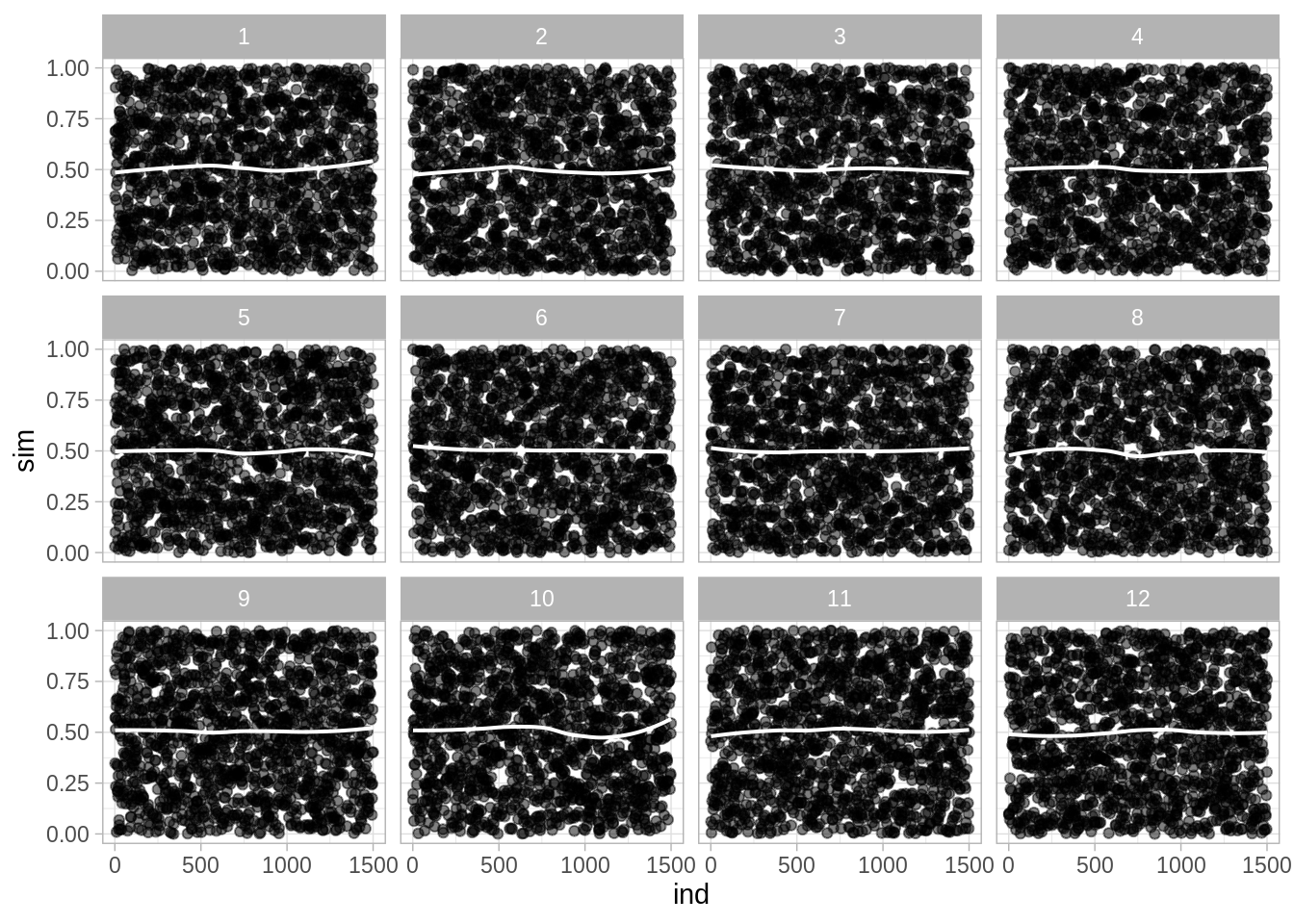
- Comparemos con los cuantiles de una uniforme:
ggplot(sucesiones) +
stat_qq(aes(sample = sim), distribution = qunif) +
geom_abline(color = "white", size = 0.6, alpha = 0.6) +
facet_wrap(~ serie) 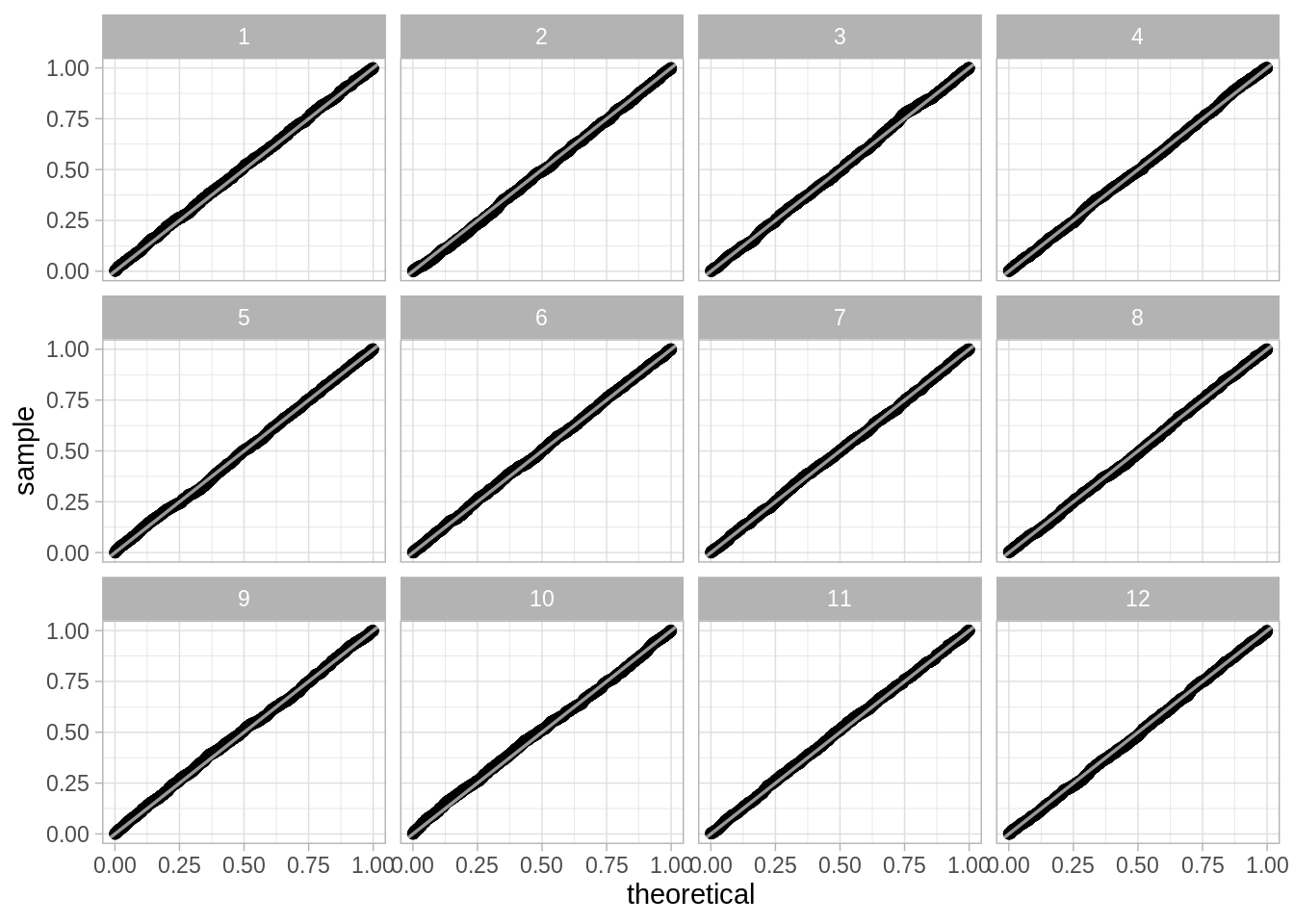
Ejemplo: RANDU
RANDU fue generador de números aleatorios ampliamente utilizado en los 60´s y 70´s, se define como:
\[X_{n + 1}= (2 ^ {16} + 3)X_n mod(2^{31})\]
A primera vista las sucesiones se asemejan a una uniforme, sin embargo, cuando se grafican ternas emergen patrones no deseados.
library(tourr)
library(plotly)
n <- 150000 # longitud de la sucesión
x <- rep(NA, n)
u <- rep(NA, n)
x[1] <- 4798373 # semilla
u[1] <- x[1] / (2 ^ 31 - 1) # transformamos al (0, 1)
for (i in 2:n) {
x[i] <- ((2 ^ 16 + 3) * x[i - 1]) %% (2 ^ 31)
u[i] <- x[i] / (2 ^ 31)
}
u_randu <- u
set.seed(8111938)
mat <- matrix(u[1:1500], ncol = 3, byrow = TRUE)
tour <- new_tour(mat, grand_tour(), NULL)
steps <- seq(0, 1, 0.01)
names(steps) <- steps
mat_xy <- map_dfr(steps, ~data.frame(center(mat %*% tour(.)$proj)),
.id = "steps")
# step 0.72
mat_xy %>%
mutate(steps = as.numeric(steps)) %>%
plot_ly(x = ~X1, y = ~X2, frame = ~steps, type = 'scatter',
mode = 'markers', showlegend = F, marker = list(size = 5,
color = "black"), opacity = 0.5) %>%
animation_opts(frame = 250)Veamos los resultados enteros del generador, ¿qué notas?
options(digits = 5)
n <- 50
x <- rep(NA, n)
x[1] <- 1 # semilla
u[1] <- x[1] # transformamos al (0, 1)
for (i in 2:n) {
x[i] <- ((2 ^ 16 + 3) * x[i - 1]) %% (2 ^ 31)
}
x
#> [1] 1 65539 393225 1769499 7077969 26542323
#> [7] 95552217 334432395 1146624417 1722371299 14608041 1766175739
#> [13] 1875647473 1800754131 366148473 1022489195 692115265 1392739779
#> [19] 2127401289 229749723 1559239569 845238963 1775695897 899541067
#> [25] 153401569 1414474403 663781353 1989836731 1670020913 701529491
#> [31] 2063890617 1774610987 662584961 888912771 1517695625 1105958811
#> [37] 1566426833 1592415347 1899101529 1357838347 1792534561 682145891
#> [43] 844966185 1077967739 1010594417 656824147 1288046073 1816859115
#> [49] 1456223681 975544643Generadores congruenciales y Mersenne-Twister
Los generadores como rand y RANDU (\(X_{n+1} = (7^5)X_n mod(2^{31}-1)\) y \(X_{n+1}= (2 ^ {16} + 3)X_n mod(2^{31})\)) se denominan generadores congruenciales.
Los Generadores Congruenciales Lineales (GCL) tienen la forma
\[X_{n+1} = (aX_n + c)mod(m)\]
Están determinados por los parámetros:
* Módulo: \(m > 0\)
* Multiplicador \(0\le a < m\)
* Incremento \(c \le m\)
* Semilla \(0\le X_0 < m\)
Los GCL se introdujeron en 1949 por D.H. Lehemer y aún son usados. La elección de los parámetros determina la calidad del generador:
Queremos \(m\) grande pues el periodo (longitud del ciclo) del generador no puede tener más de \(m\) elementos.
Queremos velocidad, en este caso, un valor conveniente para \(m\) es el tamaño de palabra (máximo número de bits que puede procesar el CPU en un ciclo) de la computadora. Los GCL más eficientes tienen \(m\) igual a una potencia de 2 (es usual 232 o 264) de esta manera la operación módulo se calcula truncando todos los dígitos excepto los últimos 32 ó 64 bits.
- ¿podemos elegir \(a\) y \(c\) de tal manera que logremos alcanzar el periodo
máximo (\(m\))?
Un generador congruencial mixto (\(c>0\)) tendrá periodo completo para todas las
semillas sí y sólo sí:
- \(m\) y \(c\) son primos relativos.
- \(a-1\) es divisible por todos los factores primos de \(m\).
- \(a-1\) es divisible por 4 si \(m\) es divisible por 4.
- \(m\) y \(c\) son primos relativos.
Vale la pena notar que un periodo grande no determina que el generador congruencial es bueno, debemos verificar que los números que generan se comportan como si fueran aleatorios. Los GCLs tienden a exhibir defectos, por ejemplo, si se utiliza un GCL para elegir puntos en un espacio de dimensión \(k\) los puntos van a caer en a lo más \((k!m)^{1/k}\) hiperplanos paralelos \(k\) dimensionales (como observamos con RANDU), donde \(k\) se refiere a la dimensión de \([0,1]^k\).
Los GCLs continuan siendo utilizados en muchas aplicaciones porque con una elección cuidadosa de los parámetros pueden pasar muchas pruebas de aleatoriedad, son rápidos y requiren poca memoria. Un ejemplo es Java, su generador de números aleatorios default java.util.Random es un GCL con multiplicador \(a=25214903917\), incremento \(c=11\) y módulo \(m=2^{48}\), sin embargo, actualmente el generador default de R es el Mersenne-Twister que no pertenece a la clase de GCLs (se puede elegir usar otros generadores para ver los disponible teclea ?Random).
El generador Mersenne-Twister se desarrolló en 1997 por Makoto Matsumoto y Takuji Nishimura (Matsumoto and Nishimura (1998)), es el generador default en muchos programas, por ejemplo, en Python, Ruby, C++ estándar, Excel y Matlab (más aquí). Este generador tiene propiedades deseables como un periodo largo (2^19937-1) y el hecho que pasa muchas pruebas de aleatoriedad; sin embargo, es lento (relativo a otros generadores) y falla algunas pruebas de aleatoreidad. .
Pruebas de aleatoriedad
Hasta ahora hemos graficado las secuencias de números aleatorios para evaluar su aleatoriedad, sin embargo, el ojo humano no es muy bueno discriminando aleatoriedad y las gráficas no escalan. Es por ello que resulta conveniente hacer pruebas estadísticas para evaluar la calidad de los generadores de números pseudoaleatorios.
Hay dos tipos de pruebas:
empíricas: evalúan estadísticas de sucesiones de números.
teóricas: se establecen las características de las sucesiones usando métodos de teoría de números con base en la regla de recurrencia que generó la sucesión.
Veremos 2 ejemplos de la primera clase: prueba de bondad de ajuste \(\chi^2\) y prueba de espera.
Ejemplo: prueba de bondad de ajuste \(\chi^2\)
\(H_0:\) Los datos son muestra de una cierta distribución \(F\).
\(H_1:\) Los datos no son una muestra de \(F\).
Procedimiento general:
- Partir el soporte de \(F\) en \(c\) celdas que son exhaustivas y mutuamente
exculyentes.
- Contar el número de observaciones en cada celda \(O_i\).
- Calcular el valor esperado en cada celda bajo \(F\): \(e_i=np_i\).
- Calcular la estadística de prueba:
\[\chi^2 = \sum_{i=1}^c \frac{(o_i - e_i)^2}{e_i} \sim \chi^2_{c-k-1}\] donde \(c\) es el número de celdas y \(k\) el número de parámetros estimados en \(F\) a partir de los datos observados.
u_rand_cat <- cut(u_rand, breaks = seq(0, 1, 0.1))
u_randu_cat <- cut(u_randu, breaks = seq(0, 1, 0.1))
u_mt <- runif(150000)
u_mt_cat <- cut(u_mt, breaks = seq(0, 1, 0.1))
chisq_test <- function(o_i) {
expected <- rep(15000, 10)
observed <- table(o_i)
x2 <- sum((observed - expected) ^ 2 / expected)
list(x2 = x2, p_value = pchisq(x2, 9))
}
chisq_test(u_rand_cat)
#> $x2
#> [1] 15.916
#>
#> $p_value
#> [1] 0.93135
chisq_test(u_randu_cat)
#> $x2
#> [1] 3.0491
#>
#> $p_value
#> [1] 0.037682
chisq_test(u_mt_cat)
#> $x2
#> [1] 17.23
#>
#> $p_value
#> [1] 0.95477Una variación de esta prueba de bondad de ajuste \(\chi^2\), es la prueba de uniformidad k-dimensional:
\(H_0:\) Distribución uniforme en \([0,1]^k\), con \(k = 1,2,...\)
En este caso se divide el espacio \([0,1]^k\) en celdas exhaustivas y mutuamente excluyentes, y se aplica la prueba \(\chi^2\) a los vectores sucesivos \((u_1,u_2,...,u_k),(u_{k+1},u_{k+2},...,u_{2k}),...\)
7.1.0.1 Ejemplo: prueba de espera
\(H_0:\) independencia y uniformidad
Procedimiento:
Seleccionar un subintervalo del \((0,1)\).
Calcular la probabilidad del subintervalo.
Ubicar en la sucesión las posiciones de los elementos que pertenezcan al subintervalo.
Calcular el número de elementos consecutivos de la sucesión entre cada una de las ocurrencias consecutivas de elementos del subintervalo (tiempos de espera).
La distribución de los tiempos de espera es geométrica con parámetro calculado en 2.
Aplicar una prueba \(\chi^2\) a los tiempos de espera.
# 1
intervalo <- c(0, 0.5)
# 2
p_intervalo <- 0.5
# 3 evaluamos u_rand
gap_u_rand <- tibble(posicion = 1:length(u_rand), u_rand = u_rand,
en_intervalo = (0.5 < u_rand & u_rand < 1))
posiciones <- gap_u_rand %>%
filter(en_intervalo) %>%
mutate(
espera = posicion - lag(posicion),
espera = ifelse(is.na(espera), posicion, espera),
espera = factor(espera, levels = 1:18)
)
# 4
gap_frec <- as.data.frame(table(posiciones$espera)) %>%
rename(espera = Var1, obs = Freq)
# esperados geométrica
gap_frec$geom <- (dgeom(0:18, p_intervalo) * length(u_rand)) [-1]
x2 <- sum((gap_frec$obs - gap_frec$geom) ^ 2 / gap_frec$geom)
pchisq(x2, 16)
#> [1] 0.91722Otras pruebas de aleatoriedad son prueba de rachas, Kolmogorov-Smirnov,
prueba de poker, puedes leer más de generadores aleatorios y pruebas en
Knuth (1997). En R hay pruebas implementadas en los paquetes randtoolboxy
RDieHarder.
Referencias
Knuth, Donald E. 1997. The Art of Computer Programming, Volume 2: Seminumerical Algorithms. Third. Boston: Addison-Wesley.
Matsumoto, Makoto, and Takuji Nishimura. 1998. “Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator.” ACM Trans. Model. Comput. Simul. 8 (1). New York, NY, USA: ACM:3–30. https://doi.org/10.1145/272991.272995.